
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 769 Атанасян — Подробные Ответы
Докажите, что если одна из высот тетраэдра проходит через точку пересечения высот противоположной грани, то и остальные высоты этого тетраэдра проходят через точки пересечения высот противоположных граней
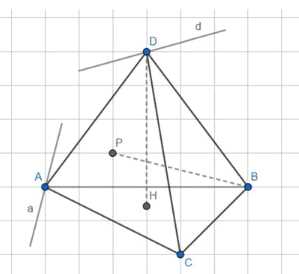
Дано: DABC — тетраэдр; DH — выс. в АВС; ВР — выс. в ADC; AH ⊥ BC; ВH ⊥ AC; CH ⊥ AB. Доказать: DH ∩ AH ∩ HC = H; BP ∩ AP ∩ PD = P. Доказательство: 1) Построим прямые a и d: d || AC, a || BC, A ∈ a и D ∈ d; 2) Так как DH ⊥ ABC, тогда: ADH ⊥ ABC, DHC ⊥ ABC, DHB ⊥ ABC; 3) По теореме о трех перпендикулярах: a || BC, AH ⊥ BC, DA ⊥ a, AD ⊥ BC; 4) Аналогично: AB ⊥ DC и AC ⊥ DB; 5) По теореме о трех перпендикулярах: AC ⊥ DB, d ⊥ DB, d ⊥ PD, PD ⊥ AC; Значит точка P лежит на высоте ΔADC; Аналогично для остальных высот.
Дано: тетраэдр DABC, высота DH в треугольнике АВС, высота ВР в треугольнике ADC, прямые AH, ВH и CH перпендикулярны соответствующим сторонам треугольника. Требуется доказать, что точки пересечения высот DH, AH и HC лежат на одной прямой, образуя высоту H, и что точки пересечения высот ВР, АР и PD лежат на одной прямой, образуя высоту P.
Доказательство:
1) Построим прямые a и d, параллельные сторонам треугольника ABC: d || AC, a || BC, при этом A ∈ a и D ∈ d.
2) Так как DH ⊥ ABC, то ADH ⊥ ABC, DHC ⊥ ABC и DHB ⊥ ABC.
3) По теореме о трех перпендикулярах, a || BC, AH ⊥ BC, DA ⊥ a и AD ⊥ BC.
4) Аналогично, AB ⊥ DC и AC ⊥ DB.
5) По теореме о трех перпендикулярах, AC ⊥ DB, d ⊥ DB, d ⊥ PD и PD ⊥ AC.
Таким образом, точка P лежит на высоте ΔADC, а точки пересечения высот DH, AH и HC лежат на одной прямой, образуя высоту H. Аналогично для остальных высот.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!