
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 768 Атанасян — Подробные Ответы
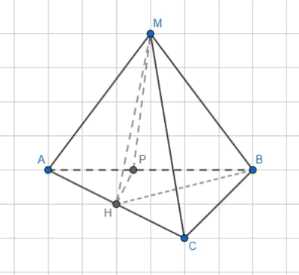
В основании пирамиды МАВС лежит треугольник АВС, в котором \(\angle C = 90°\), \(AC = 4\) см, \(BC = 3\) см. Грань МАС перпендикулярна к плоскости основания, а две другие боковые грани составляют равные углы с плоскостью основания. Расстояние от основания высоты МН пирамиды до грани МВС равно \(\frac{3}{2}\) см. Найдите площадь боковой поверхности пирамиды.
Дано: МАВС — пирамида, ∠C = 90°, AC = 4 см, BC = 3 см, MAC ⊥ ABC, ρ(H,MBC) = 4:3.
Решение: 1) ∠C = 90°, AC ⊥ CB, BC ⊥ MC; 2) AMC ⊥ ACB, MH ⊥ ABC, MH ∈ MAC; 3) PE ⊥ AB, HP ⊥ AB, MP ⊥ AB; 4) ∠MPH = ∠AMCH, ∠MBC = 2∠MBP, ΔAMH ≅ ΔΡΜΗ, ΔOMB ≅ ΔΡΜΒ, PH = CH, PB = BC, MP = MC; 5) AB = √(AC^2 + BC^2) = √25 = 5, ∠PBH = ∠CB, AB — CB = AH, CH = 5/3, AH = 4 — CH, 12 — 3CH = 5CH, 8CH = 12, CH = 1,5; 6) \(V = \frac{1}{3} \cdot S_{\text{осн}} \cdot h = \frac{1}{3} \cdot \frac{1}{2} \cdot 4 \cdot 3 = 4\), \(V_{\text{MBC}} = \frac{1}{3} \cdot MH \cdot S_{\text{MBC}} = \frac{1}{3} \cdot \frac{3}{4} \cdot 4 = 1\); 7) \(MC^2 = CH^2 + MH^2 = 1,5^2 + \left(\frac{3}{4}\right)^2 = \frac{9}{4}\), \(MP = MC = \frac{\sqrt{9}}{2} = \frac{3}{2}\); 8) \(S_{\text{MCE}} = \frac{1}{2} \cdot MC \cdot BC = \frac{1}{2} \cdot \frac{3}{2} \cdot 3 = \frac{9}{4}\), \(S_{\text{AMB}} = \frac{1}{2} \cdot AB \cdot MP = \frac{1}{2} \cdot 5 \cdot \frac{3}{2} = \frac{15}{4}\), \(S_{\text{AMC}} = \frac{1}{2} \cdot AC \cdot MH = \frac{1}{2} \cdot 4 \cdot \frac{3}{4} = 3\); 9) \(S_{\text{бок}} = 2(S_{\text{AMB}} + S_{\text{AMC}}) = 2\left(\frac{15}{4} + 3\right) = 27\). Ответ: 3(2√2 + 1).
Дано: пирамида МАВС, ∠C = 90°, AC = 4 см, BC = 3 см, MAC ⊥ ABC, ρ(H,MBC) = 4:3. Требуется найти объем пирамиды и площадь ее боковой поверхности.
Решение:
1) Поскольку ∠C = 90°, то AC ⊥ CB и BC ⊥ MC. Это следует из свойств прямоугольного треугольника.
2) Плоскости АМС и АСВ перпендикулярны, так как AMC ⊥ ACB, MH ⊥ ABC, и MH лежит в плоскости MAC.
3) Из свойств перпендикулярности следует, что PE ⊥ AB, HP ⊥ AB, MP ⊥ AB.
4) Так как ΔАМН ≅ ΔΡΜΗ и ΔΟΜВ ≅ ΔΡΜВ, то ∠MPH = ∠AMCH и ∠MBC = 2∠MBP. Также PH = CH, PB = BC, MP = MC.
5) В прямоугольном ΔАВС: AB = √(AC^2 + BC^2) = √25 = 5. Так как ∠PBH = ∠CB, то AB — CB = AH, CH = 5/3, AH = 4 — CH, 12 — 3CH = 5CH, 8CH = 12, CH = 1,5.
6) Объем пирамиды МИВС вычисляется по формуле \(V = \frac{1}{3} \cdot S_{\text{осн}} \cdot h = \frac{1}{3} \cdot \frac{1}{2} \cdot 4 \cdot 3 = 4\). Объем пирамиды MBC равен \(V_{\text{MBC}} = \frac{1}{3} \cdot MH \cdot S_{\text{MBC}} = \frac{1}{3} \cdot \frac{3}{4} \cdot 4 = 1\).
7) В прямоугольном ΔМСН: \(MC^2 = CH^2 + MH^2 = 1,5^2 + \left(\frac{3}{4}\right)^2 = \frac{9}{4}\), \(MP = MC = \frac{\sqrt{9}}{2} = \frac{3}{2}\).
8) Площади треугольников: \(S_{\text{MCE}} = \frac{1}{2} \cdot MC \cdot BC = \frac{1}{2} \cdot \frac{3}{2} \cdot 3 = \frac{9}{4}\), \(S_{\text{AMB}} = \frac{1}{2} \cdot AB \cdot MP = \frac{1}{2} \cdot 5 \cdot \frac{3}{2} = \frac{15}{4}\), \(S_{\text{AMC}} = \frac{1}{2} \cdot AC \cdot MH = \frac{1}{2} \cdot 4 \cdot \frac{3}{4} = 3\).
9) Площадь боковой поверхности пирамиды: \(S_{\text{бок}} = 2(S_{\text{AMB}} + S_{\text{AMC}}) = 2\left(\frac{15}{4} + 3\right) = 27\).
Ответ: 3(2√2 + 1).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!