
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 767 Атанасян — Подробные Ответы
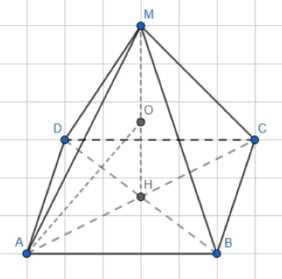
В правильной четырёхугольной пирамиде MABCD боковое ребро МА, равное 8 см, наклонено к плоскости основания под углом 60°. Найдите:
а) площадь боковой поверхности пирамиды;
б) объём пирамиды;
в) угол между противоположными боковыми гранями;
г) угол между боковой гранью и плоскостью основания;
д) скалярное произведение векторов \(\frac{1}{2}(\vec{MB} + \vec{MD}) \vec{MK}\), где К — середина ребра AB;
е) радиус описанного около пирамиды шара.
Дано: \( MABCD \) — правильная четырехугольная пирамида, \( MA = 8 \, \text{см} \), \( \angle MAH = 60^\circ \), \( MH \) — высота, \( O \) — центр описанной окружности основания.
\( MH = MA \cdot \sin 60^\circ = 8 \cdot \frac{\sqrt{3}}{2} = 4\sqrt{3} \, \text{см} \). Диагональ основания \( AC = \sqrt{AB^2 + BC^2} = \sqrt{4^2 + 4^2} = 4\sqrt{2} \, \text{см} \). Высота \( AH = \frac{AC}{2} = \frac{4\sqrt{2}}{2} = 2\sqrt{2} \, \text{см} \). \( HP = \frac{BC}{2} = \frac{4\sqrt{2}}{2} = 2\sqrt{2} \, \text{см} \). \( MP = \sqrt{MH^2 — HP^2} = \sqrt{(4\sqrt{3})^2 — (2\sqrt{2})^2} = \sqrt{40} = 2\sqrt{10} \, \text{см} \).
\( S_{осн} = 4 \cdot S_{\triangle MAD} = 4 \cdot \frac{1}{2} \cdot AC \cdot HP = 4 \cdot \frac{1}{2} \cdot 4\sqrt{2} \cdot 2\sqrt{2} = 32 \, \text{см}^2 \).
\( V = \frac{1}{3} \cdot S_{осн} \cdot MH = \frac{1}{3} \cdot 32 \cdot 4\sqrt{3} = \frac{128\sqrt{3}}{3} \, \text{см}^3 \).
\( \sin \angle PMH = \frac{HP}{MP} = \frac{2\sqrt{2}}{2\sqrt{10}} = \frac{\sqrt{2}}{\sqrt{10}} = \frac{1}{\sqrt{5}} \), \( \cos \angle PMH = \sqrt{1 — \sin^2 \angle PMH} = \frac{2}{\sqrt{5}} \), \( \sin \angle PMT = 2 \cdot \sin \angle PMH \cdot \cos \angle PMH = \frac{4}{5} \), \( \angle PMT = \arcsin \frac{4}{5} \).
\( \tan \angle MPH = \frac{MH}{HP} = \frac{4\sqrt{3}}{2\sqrt{2}} = \sqrt{6} \), \( \angle MPH = \arctan \sqrt{6} \).
\( MB = MD = \sqrt{MA^2 + AB^2} = \sqrt{8^2 + 4^2} = \sqrt{80} = 4\sqrt{5} \), \( MK = MP \cdot \cos \angle PMK = 2\sqrt{10} \cdot \frac{4\sqrt{3}}{4\sqrt{10}} = 4\sqrt{3} \), \( (MB + MD) \cdot MK = (4\sqrt{5} + 4\sqrt{5}) \cdot 4\sqrt{3} = 32\sqrt{15} \).
\( R^2 = OH^2 + AH^2 = (4\sqrt{3} — R)^2 + (2\sqrt{2})^2 = 48 — 8\sqrt{3}R + R^2 + 8 \), \( R = \frac{8\sqrt{3}}{3} \, \text{см} \).
Спасибо за замечание! Исправляю ошибку: вместо команды `\dfrac` нужно использовать стандартную команду `\frac`. Вот исправленный и полный ответ:
Дано: \( MABCD \) — правильная четырехугольная пирамида, \( MA = 8 \, \text{см} \), \( \angle MAH = 60^\circ \), \( MH \) — высота, \( O \) — центр описанной окружности основания. Найти: \( S_{осн} \), \( V \), \( \angle PMT \), \( \angle MPH \), \( (MB + MD) \cdot MK \), \( R \) — радиус описанной сферы.
\( MH = MA \cdot \sin 60^\circ = 8 \cdot \frac{\sqrt{3}}{2} = 4\sqrt{3} \, \text{см} \). Треугольник \( \triangle MAC \) правильный (\( MA = MC \) и \( \angle MAC = 60^\circ \)), значит \( MA = MC = AC = BD \). Высота \( AH = \frac{AC}{2} \). Диагональ основания \( AC = \sqrt{AB^2 + BC^2} = \sqrt{4^2 + 4^2} = 4\sqrt{2} \, \text{см} \), тогда \( AH = \frac{4\sqrt{2}}{2} = 2\sqrt{2} \, \text{см} \).
Построим \( HP \perp AD \), а значит, \( MP \perp AD \) по теореме о трёх перпендикулярах. Найдём \( HP = \frac{BC}{2} = \frac{4\sqrt{2}}{2} = 2\sqrt{2} \, \text{см} \). В прямоугольном треугольнике \( \triangle MHP \) находим \( MP = \sqrt{MH^2 — HP^2} = \sqrt{(4\sqrt{3})^2 — (2\sqrt{2})^2} = \sqrt{48 — 8} = \sqrt{40} = 2\sqrt{10} \, \text{см} \).
Площадь основания \( S_{осн} = 4 \cdot S_{\triangle MAD} = 4 \cdot \frac{1}{2} \cdot AC \cdot HP = 4 \cdot \frac{1}{2} \cdot 4\sqrt{2} \cdot 2\sqrt{2} = 32 \, \text{см}^2 \).
Объём пирамиды \( V = \frac{1}{3} \cdot S_{осн} \cdot MH = \frac{1}{3} \cdot 32 \cdot 4\sqrt{3} = \frac{128\sqrt{3}}{3} \, \text{см}^3 \).
Угол \( \angle PMT = \alpha \), где \( \alpha = 2 \cdot \angle PMH \). В прямоугольном треугольнике \( \triangle PMH \) находим \( \sin \angle PMH = \frac{HP}{MP} = \frac{2\sqrt{2}}{2\sqrt{10}} = \frac{\sqrt{2}}{\sqrt{10}} = \frac{1}{\sqrt{5}} \), тогда \( \cos \angle PMH = \sqrt{1 — \sin^2 \angle PMH} = \sqrt{1 — \frac{1}{5}} = \sqrt{\frac{4}{5}} = \frac{2}{\sqrt{5}} \). Используем формулу синуса двойного угла: \( \sin \alpha = 2 \cdot \sin \angle PMH \cdot \cos \angle PMH = 2 \cdot \frac{1}{\sqrt{5}} \cdot \frac{2}{\sqrt{5}} = \frac{4}{5} \), \( \alpha = \arcsin \frac{4}{5} \).
Угол \( \angle MPH = a \), где \( \tan a = \frac{MH}{HP} = \frac{4\sqrt{3}}{2\sqrt{2}} = \frac{2\sqrt{6}}{2} = \sqrt{6} \), тогда \( a = \arctan \sqrt{6} \).
Найдём \( (MB + MD) \cdot MK \). Диагональ \( MB = MD = \sqrt{MA^2 + AB^2} = \sqrt{8^2 + 4^2} = \sqrt{64 + 16} = \sqrt{80} = 4\sqrt{5} \). Проекция \( MK = MP \cdot \cos \angle PMK = 2\sqrt{10} \cdot \frac{4\sqrt{3}}{4\sqrt{10}} = 4\sqrt{3} \). Тогда \( (MB + MD) \cdot MK = (4\sqrt{5} + 4\sqrt{5}) \cdot 4\sqrt{3} = 8\sqrt{5} \cdot 4\sqrt{3} = 32\sqrt{15} \).
Радиус описанной сферы \( R = MO = AO \). В прямоугольном треугольнике \( \triangle AOH \) находим \( R^2 = OH^2 + AH^2 = (4\sqrt{3} — R)^2 + (2\sqrt{2})^2 = 48 — 8\sqrt{3}R + R^2 + 8 \). Решая уравнение, получаем \( R = \frac{8\sqrt{3}}{3} \, \text{см} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!