
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 766 Атанасян — Подробные Ответы
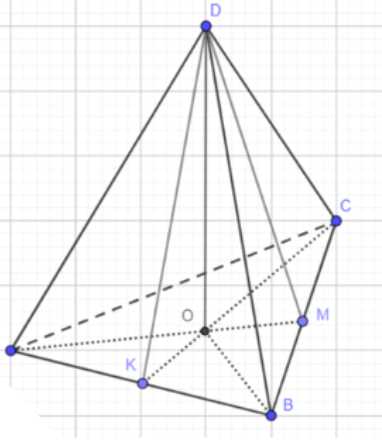
В правильной треугольной пирамиде DABC высота DO равна 3 см, а боковое ребро DA равно 5 см. Найдите:
а) площадь полной поверхности пирамиды;
б) объём пирамиды;
в) угол между боковым ребром и плоскостью основания;
г) угол наклона боковой грани к плоскости основания;
д) скалярное произведение векторов \(\frac{1}{2}(\vec{DB} + \vec{DC}) \vec{MA}\), где М — середина ребра ВС;
е) радиус шара, вписанного в пирамиду.
а) В прямоугольном треугольнике AOD:
\(AO = \sqrt{AD^2 — DO^2} = \sqrt{25 — 9} = 4 \text{ см}\)
Так как треугольник ABC равносторонний, то \(AO\) является радиусом описанной окружности:
\(R = AO = \frac{AB}{\sqrt{3}}, \text{ откуда } AB = AO\sqrt{3} = 4\sqrt{3} \text{ см}\)
\(S_{ABC} = \frac{1}{2}AB \cdot BC \cdot \sin 60^\circ = \frac{1}{2} \cdot 4\sqrt{3} \cdot 4\sqrt{3} \cdot \frac{\sqrt{3}}{2} = 12\sqrt{3} \text{ см}^2\)
В треугольнике ADB опустим высоту DH, тогда в прямоугольном треугольнике ADH:
\(DH = \sqrt{AD^2 — AH^2} = \sqrt{25 — (2\sqrt{3})^2} = \sqrt{13} \text{ см}\)
\(S_{ADB} = DH \cdot AH = \sqrt{13} \cdot 2\sqrt{3} \text{ см}^2\)
\(S_{total} = 3S_{ADB} + S_{ABC} = 3 \cdot 2\sqrt{3} \cdot \sqrt{13} + 12\sqrt{3} = 6\sqrt{3}(2\sqrt{13} + 4) \text{ см}^2\)
Решение:
б) Объем пирамиды: \(V = \frac{1}{3} D_0 \cdot S_{ABC} = \frac{1}{3} \cdot 3 \cdot 12\sqrt{3} = 12\sqrt{3} \text{ см}^3\)
в) Искомый угол \(\angle DAO = a\): в прямоугольном треугольнике \(\triangle ADO\), \(\sin a = \frac{DO}{AD} = \frac{3}{5} = 0,6\), отсюда \(a = \arcsin 0,6\)
г) \(DH \in DAB\) и \(HO \in ABCD\), значит \(\angle (DAB)(ABCD) = 2\angle DHO = a\); в прямоугольном треугольнике \(\triangle ADH\), \(OH = \sqrt{A_0^2 — AH^2} = \sqrt{16 — (2\sqrt{3})^2} = \sqrt{4} = 2 \text{ см}\)
в прямоугольном треугольнике \(\triangle ADH\), \(\tan a = \frac{DO}{OH} = \frac{3}{2} = 1,5\), отсюда \(a = \arctan 1,5\)
д) \(\frac{1}{2}(DB + DC) \cdot MA = DM \cdot MA\), \(OM = OH = 2 \text{ см}\) и \(MA = \frac{S_{ABC}}{AB} = \frac{12\sqrt{3}}{2\sqrt{3}} = 6 \text{ см}\)
\(DM \cdot MA \cdot \cos \angle DMA = DM \cdot 6 = 6 \cdot OM = 6 \cdot 2 = 12\)
е) \(V_{\text{пир}} = \frac{1}{3} S_{\text{пов}} \cdot R_{\text{вписанной}}\), \(R = \frac{3 \cdot 12\sqrt{3}}{6\sqrt{3} \cdot (\sqrt{13} + 2)} = \frac{6}{\sqrt{13} + 2} \text{ см}\)
Задача состоит в нахождении площади прямоугольного треугольника AOD, площади равностороннего треугольника ABC, а также общей площади фигуры.
Шаг 1. Найдем длину стороны AO прямоугольного треугольника AOD.
Из условия задачи известно, что \(AD = 5\) см и \(DO = 3\) см.
Применим теорему Пифагора для прямоугольного треугольника AOD:
\(AO = \sqrt{AD^2 — DO^2} = \sqrt{25 — 9} = \sqrt{16} = 4\) см
Шаг 2. Найдем длину стороны AB равностороннего треугольника ABC.
Так как треугольник ABC равносторонний, то \(AO\) является радиусом описанной окружности.
Используем формулу для радиуса описанной окружности равностороннего треугольника:
\(R = \frac{AB}{\sqrt{3}}\)
Отсюда:
\(AB = R\sqrt{3} = 4\sqrt{3}\) см
Шаг 3. Найдем площадь равностороннего треугольника ABC.
Площадь равностороннего треугольника вычисляется по формуле:
\(S_{ABC} = \frac{1}{2}ab\sin C\)
Где \(a = b = AB = 4\sqrt{3}\) см, \(\sin C = \frac{\sqrt{3}}{2}\).
Подставляя значения, получаем:
\(S_{ABC} = \frac{1}{2} \cdot 4\sqrt{3} \cdot 4\sqrt{3} \cdot \frac{\sqrt{3}}{2} = 12\sqrt{3}\) см^2
Шаг 4. Найдем высоту DH треугольника ADB.
Опустим высоту DH на сторону AB треугольника ADB.
В прямоугольном треугольнике ADH:
\(DH = \sqrt{AD^2 — AH^2} = \sqrt{25 — (2\sqrt{3})^2} = \sqrt{13}\) см
Шаг 5. Найдем площадь треугольника ADB.
Площадь треугольника вычисляется по формуле:
\(S_{ADB} = \frac{1}{2}bh\)
Где \(b = AH = 2\sqrt{3}\) см, \(h = DH = \sqrt{13}\) см.
Подставляя значения, получаем:
\(S_{ADB} = \frac{1}{2} \cdot 2\sqrt{3} \cdot \sqrt{13} = \sqrt{13} \cdot 2\sqrt{3}\) см^2
Шаг 6. Найдем общую площадь фигуры.
Общая площадь фигуры равна сумме площадей треугольников ABC и ADB:
\(S_{total} = S_{ABC} + 3S_{ADB} = 12\sqrt{3} + 3\sqrt{13} \cdot 2\sqrt{3} = 6\sqrt{3}(2\sqrt{13} + 4)\) см^2
Решение:
б) Объем пирамиды:
Формула объема пирамиды: \(V = \frac{1}{3} D_0 \cdot S_{ABC}\), где \(D_0\) — основание пирамиды, \(S_{ABC}\) — площадь основания. В условии задачи дано, что \(D_0 = 3\) и \(S_{ABC} = 12\sqrt{3}\). Подставляя эти значения в формулу, получаем:
\(V = \frac{1}{3} \cdot 3 \cdot 12\sqrt{3} = 12\sqrt{3} \text{ см}^3\)
в) Искомый угол \(\angle DAO = a\):
Для нахождения угла \(a\) используем прямоугольный треугольник \(\triangle ADO\). Согласно условию, \(\sin a = \frac{DO}{AD}\). Из треугольника видно, что \(DO = 3\) и \(AD = 5\). Подставляя эти значения, получаем:
\(\sin a = \frac{3}{5} = 0,6\)
Отсюда, \(a = \arcsin 0,6\)
г) \(DH \in DAB\) и \(HO \in ABCD\):
Так как \(DH \in DAB\) и \(HO \in ABCD\), то \(\angle (DAB)(ABCD) = 2\angle DHO = a\). Для нахождения \(OH\) используем прямоугольный треугольник \(\triangle ADH\). Согласно теореме Пифагора:
\(OH = \sqrt{A_0^2 — AH^2} = \sqrt{16 — (2\sqrt{3})^2} = \sqrt{4} = 2 \text{ см}\)
Далее, в прямоугольном треугольнике \(\triangle ADH\) находим \(\tan a = \frac{DO}{OH} = \frac{3}{2} = 1,5\), отсюда \(a = \arctan 1,5\)
д) \(\frac{1}{2}(DB + DC) \cdot MA = DM \cdot MA\):
Согласно условию, \(OM = OH = 2 \text{ см}\) и \(MA = \frac{S_{ABC}}{AB} = \frac{12\sqrt{3}}{2\sqrt{3}} = 6 \text{ см}\)
Теперь можно найти \(DM \cdot MA \cdot \cos \angle DMA\):
\(DM \cdot MA \cdot \cos \angle DMA = DM \cdot 6 = 6 \cdot OM = 6 \cdot 2 = 12\)
е) \(V_{\text{пир}} = \frac{1}{3} S_{\text{пов}} \cdot R_{\text{вписанной}}\):
Для нахождения \(R_{\text{вписанной}}\) используем формулу:
\(R = \frac{3 \cdot 12\sqrt{3}}{6\sqrt{3} \cdot (\sqrt{13} + 2)} = \frac{6}{\sqrt{13} + 2} \text{ см}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!