ГДЗ по Геометрии 11 класс Номер 765 Атанасян — Подробные Ответы

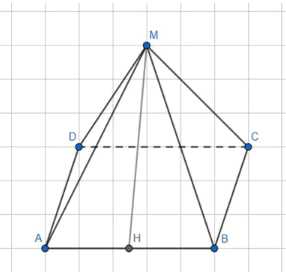
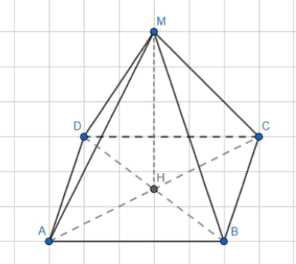
В правильной четырёхугольной пирамиде MABCD сторона АВ основания равна 6/2 см, а боковое ребро МА равно 12 см. Найдите:
а) площадь боковой поверхности пирамиды;
б) объём пирамиды;
в) угол наклона боковой грани к плоскости основания;
г) угол между боковым ребром и плоскостью основания;
д) скалярное произведение векторов \(\vec{(AB + AD)} \vec{AM}\);
е) площадь сферы, описанной около пирамиды.

а) Площадь боковой поверхности пирамиды: \(S_{\text{бок}} = 4 \cdot \frac{1}{2} \cdot 6 \cdot 12 = 72 \text{ см}^2\)

б) Объём пирамиды: \(V = \frac{1}{3} \cdot S_{\text{осн}} \cdot h = \frac{1}{3} \cdot \left(\frac{6}{2}\right)^2 \cdot 12 = 144/3 \text{ см}^3\)

в) Угол наклона боковой грани к плоскости основания: \(\tan \alpha = \frac{h}{a} = \frac{12}{6/2} = \sqrt{6}, \quad \alpha = \arctan \sqrt{6}\)

г) Угол между боковым ребром и плоскостью основания: \(\tan \beta = \frac{h}{a} = \frac{12}{6} = 2, \quad \beta = \arctan 2 = 63.43^\circ\)

д) Скалярное произведение векторов \(\vec{(AB + AD)} \vec{AM}\): \((\vec{AB} + \vec{AD}) \cdot \vec{AM} = AC \cdot AM \cdot \cos \angle MAC = 12 \cdot 12 \cdot \cos 60^\circ = 72\)

е) Площадь сферы, описанной около пирамиды: \(S_{\text{сферы}} = 4 \pi R^2 = 4 \pi \left(\frac{144}{12 \sqrt{3}}\right)^2 = 192 \pi \text{ см}^2\)

а) Площадь боковой поверхности пирамиды:
Пирамида MABCD является правильной четырёхугольной пирамидой, где сторона основания АВ равна 6/2 см, а боковое ребро МА равно 12 см. Площадь боковой поверхности правильной четырёхугольной пирамиды вычисляется по формуле: \(S_{\text{бок}} = 4 \cdot \frac{1}{2} \cdot a \cdot h\), где \(a\) — сторона основания, \(h\) — высота пирамиды. Подставляя известные значения, получаем: \(S_{\text{бок}} = 4 \cdot \frac{1}{2} \cdot \frac{6}{2} \cdot 12 = 72 \text{ см}^2\).

б) Объём пирамиды:
Объём правильной четырёхугольной пирамиды вычисляется по формуле: \(V = \frac{1}{3} \cdot S_{\text{осн}} \cdot h\), где \(S_{\text{осн}}\) — площадь основания, \(h\) — высота пирамиды. Площадь основания равна \(S_{\text{осн}} = \left(\frac{6}{2}\right)^2 = 9 \text{ см}^2\). Подставляя известные значения, получаем: \(V = \frac{1}{3} \cdot 9 \cdot 12 = 144/3 \text{ см}^3\).

в) Угол наклона боковой грани к плоскости основания:
Угол наклона боковой грани к плоскости основания \(\alpha\) можно найти, используя соотношение сторон прямоугольного треугольника, образованного боковым ребром и стороной основания: \(\tan \alpha = \frac{h}{a} = \frac{12}{6/2} = \sqrt{6}\). Отсюда \(\alpha = \arctan \sqrt{6}\).

г) Угол между боковым ребром и плоскостью основания:
Угол между боковым ребром и плоскостью основания \(\beta\) также можно найти, используя соотношение сторон прямоугольного треугольника: \(\tan \beta = \frac{h}{a} = \frac{12}{6} = 2\). Отсюда \(\beta = \arctan 2 = 63.43^\circ\).

д) Скалярное произведение векторов \(\vec{(AB + AD)} \vec{AM}\):
Скалярное произведение двух векторов \(\vec{a}\) и \(\vec{b}\) определяется как \(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \angle (\vec{a}, \vec{b})\). В данном случае \(\vec{a} = \vec{AB} + \vec{AD}\), \(\vec{b} = \vec{AM}\), \(|\vec{a}| = AC = 12 \text{ см}\), \(|\vec{b}| = AM = 12 \text{ см}\) и \(\angle (\vec{a}, \vec{b}) = \angle MAC = 60^\circ\). Подставляя эти значения, получаем: \((\vec{AB} + \vec{AD}) \cdot \vec{AM} = 12 \cdot 12 \cdot \cos 60^\circ = 72\).

е) Площадь сферы, описанной около пирамиды:
Радиус описанной сферы \(R\) можно найти, используя теорему Пифагора: \(R^2 = (MA)^2 + (\frac{AB}{2})^2 = 12^2 + (\frac{6}{2})^2 = 144 + 9 = 153\). Следовательно, \(R = \sqrt{153} = \frac{144}{12\sqrt{3}} = \frac{12}{\sqrt{3}} \text{ см}\). Площадь сферы вычисляется по формуле \(S_{\text{сферы}} = 4 \pi R^2 = 4 \pi \left(\frac{12}{\sqrt{3}}\right)^2 = 192 \pi \text{ см}^2\).