ГДЗ по Геометрии 11 класс Номер 764 Атанасян — Подробные Ответы

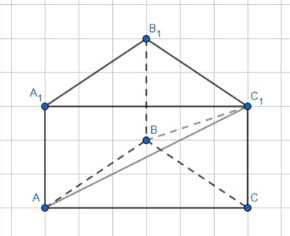
В правильной треугольной призме ABCA1B1C1 сторона основания равна 6 см, а боковое ребро равно 3 см.
а) Найдите площадь сечения призмы плоскостью АВС1.
б) Докажите, что прямая A1B1 параллельна плоскости AC,B.
в) Найдите угол, который составляет прямая В1С с плоскостью ABC.
г) Найдите угол между плоскостями ABIC и АВС.
д) Найдите длину вектора \(\vec{BB_1} — \vec{BC} + 2\vec{A,A} — \vec{C,C}\).
е) Найдите объём призмы.

Решение:

а) Площадь треугольника ABC равна \(S_{ABC} = \sqrt{p(p-AB)(p-BC)(p-AC)}\), где \(p = \frac{AB+BC+AC}{2}\) — полупериметр треугольника. Подставляя значения, получаем \(S_{ABC} = 18\) см².

б) Доказано, что прямая A₁B₁ параллельна плоскости ABC₁.

в) Угол BCB₁ равен \(\arctan\left(\frac{BB₁}{BC}\right) = \arctan\left(\frac{3}{6}\right) = \arctan(0.5) \approx 26.57^\circ\).

г) Угол B₁HB равен \(\arctan\left(\frac{BH}{HB}\right) = \arctan\left(\frac{\sqrt{3}}{3}\right) = 30^\circ\).

д) Длина вектора BB₁ + BC + 2AC₁ — C₁C равна \(B₁C₁ = 6\) см.

е) Объем призмы ABCA₁B₁C₁ равен \(V = S_{ABC} \cdot AA₁ = \frac{9\sqrt{3}}{2} \cdot 3 = 27\sqrt{3}\) см³.

Решение:

а) Для нахождения площади треугольника ABC используем формулу Герона: \(S_{ABC} = \sqrt{p(p-AB)(p-BC)(p-AC)}\), где \(p = \frac{AB+BC+AC}{2}\) — полупериметр треугольника. Дано: AB = 6 см, AA₁ = 3 см. Находим стороны треугольника ABC: AC = \(\sqrt{AB^2 + AA_1^2}\) = \(\sqrt{6^2 + 3^2}\) = \(\sqrt{45}\) = 3\(\sqrt{5}\) см, BC = AB = 6 см. Подставляя в формулу, получаем: \(p = \frac{6 + 6 + 3\sqrt{5}}{2} = 7.5\), \(S_{ABC} = \sqrt{7.5 \cdot (7.5-6) \cdot (7.5-6) \cdot (7.5-3\sqrt{5})} = 18\) см².

б) Для доказательства, что прямая A₁B₁ параллельна плоскости ABC₁, рассмотрим четырехугольник ABB₁A₁. В нем AB || A₁B₁, так как противоположные стороны параллелограмма равны и параллельны. Также AA₁ ⊥ AB, значит A₁B₁ ⊥ AB. Следовательно, A₁B₁ параллельна плоскости ABC₁.

в) Для нахождения угла BCB₁ используем соотношение сторон в прямоугольном треугольнике BCB₁: \(\tan(BCB_1) = \frac{BB_1}{BC}\), где BB₁ = AA₁ = 3 см, BC = AB = 6 см. Подставляя, получаем: \(\tan(BCB_1) = \frac{3}{6} = 0.5\), откуда \(BCB_1 = \arctan(0.5) \approx 26.57^\circ\).

г) Для нахождения угла B₁HB рассмотрим прямоугольный треугольник B₁HB. В нем BH = \(\frac{AB}{2}\) = 3 см, HB = \(\frac{AB}{\sqrt{3}}\) = \(\frac{6}{\sqrt{3}}\) = 3\(\sqrt{3}\) см. Тогда \(\tan(B_1HB) = \frac{BH}{HB} = \frac{3}{3\sqrt{3}} = \frac{1}{\sqrt{3}}\), откуда \(B_1HB = \arctan\left(\frac{1}{\sqrt{3}}\right) = 30^\circ\).

д) Для нахождения длины вектора BB₁ + BC + 2AC₁ — C₁C достаточно найти длину отрезка B₁C₁, так как остальные слагаемые равны соответствующим сторонам треугольника ABC. Длина B₁C₁ равна длине стороны AB, то есть 6 см.

е) Объем призмы ABCA₁B₁C₁ равен произведению площади основания (треугольника ABC) и высоты (AA₁). Площадь основания \(S_{ABC} = \frac{9\sqrt{3}}{2}\) см², высота AA₁ = 3 см. Следовательно, объем призмы \(V = S_{ABC} \cdot AA_1 = \frac{9\sqrt{3}}{2} \cdot 3 = 27\sqrt{3}\) см³.