
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 760 Атанасян — Подробные Ответы
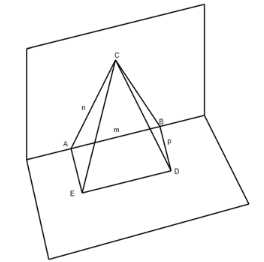
Отрезки СА и DB перпендикулярны к ребру двугранного угла CABD, равного 120°. Известно, что \(AB= m\), \(CA = n\), \(BD= p\). Найдите \(CD\)
Согласно теореме косинусов, для треугольника САЕ имеем: \(CF^2 = AC^2 + AE^2 — 2AC \cdot AE \cdot \cos 120° = n^2 + p^2 + np\). Для прямоугольного треугольника CED, по теореме Пифагора: \(CD = \sqrt{CE^2 + ED^2} = \sqrt{n^2 + p^2 + m^2 + np}\).
Дан прямоугольник AEDB, где AE=BD=p и AB=ED=m. Рассмотрим треугольник CAE.
Для нахождения длины стороны CF в треугольнике CAE можно применить теорему косинусов:
\(CF^2 = AC^2 + AE^2 — 2AC \cdot AE \cdot \cos 120°\)
Где:
— AC = n (длина стороны AC)
— AE = p (длина стороны AE)
— Угол между сторонами AC и AE равен 120°, поэтому \(\cos 120° = -\frac{1}{2}\)
Подставляя значения, получаем:
\(CF^2 = n^2 + p^2 — 2np \cdot (-\frac{1}{2}) = n^2 + p^2 + np\)
Таким образом, длина стороны CF равна \(\sqrt{n^2 + p^2 + np}\).
Теперь рассмотрим прямоугольный треугольник CED. Применяя теорему Пифагора, можно найти длину гипотенузы CD:
\(CD = \sqrt{CE^2 + ED^2} = \sqrt{n^2 + p^2 + m^2 + np}\)
Таким образом, мы получили выражения для длин сторон треугольников CAE и CED, используя исходные данные — длины сторон прямоугольника AEDB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!