ГДЗ по Геометрии 11 класс Номер 758 Атанасян — Подробные Ответы

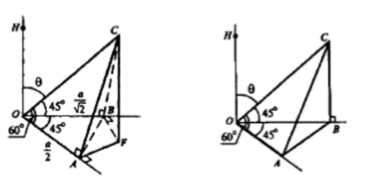
Лучи ОА, ОВ и ОС расположены так, что \(\angle BOC = \angle BOA = 45°\), \(\angle AOC = 60°\). Прямая ОН перпендикулярна к плоскости АОВ. Найдите угол между прямыми ОН и ОС.

Рассмотрим треугольник СОА: \(OA = OC \cos 60° = \frac{OC}{2}\)
Рассмотрим треугольник СОВ: \(OB = OC \cos 45° = \frac{OC}{\sqrt{2}}\)
Рассмотрим треугольник АОВ.
По теореме косинусов: \(AB^2 = OB^2 + OA^2 — 2OB \cdot AO \cos 45°\)
\(AB^2 = \frac{OC^2}{2} + \frac{OC^2}{2} — 2 \cdot \frac{OC}{\sqrt{2}} \cdot \frac{OC}{\sqrt{2}} \cdot \cos 45°\)
\(AB^2 = OC^2 — OC^2 \cdot \cos 45° = OC^2 \left(1 — \cos 45°\right) = \frac{OC^2}{2}\)
\(AB = \frac{OC}{\sqrt{2}}\)
Таким образом, треугольник АОВ равнобедренный, \(OA = AB\).
Прямые НО и СВ перпендикулярны к плоскости АВО, то есть они лежат в одной плоскости, \(\angle HOB = 90°\), \(\angle COB = 45°\). Следовательно, искомый угол равен 45 градусов.

Рассмотрим треугольник СОА. Согласно рисунку, сторона ОА является одной из сторон этого треугольника. Для нахождения длины ОА воспользуемся тригонометрическим тождеством:

\(OA = OC \cos 60°\)

Где \(OC\) — длина стороны ОС треугольника СОА. Подставляя значение угла 60°, получаем:

\(OA = OC \cdot \frac{1}{2} = \frac{OC}{2}\)

Таким образом, длина стороны ОА равна половине длины стороны ОС.

Далее рассмотрим треугольник СОВ. Согласно рисунку, сторона ОВ является одной из сторон этого треугольника. Для нахождения длины ОВ воспользуемся тригонометрическим тождеством:

\(OB = OC \cos 45°\)

Где \(OC\) — длина стороны ОС треугольника СОВ. Подставляя значение угла 45°, получаем:

\(OB = OC \cdot \frac{1}{\sqrt{2}} = \frac{OC}{\sqrt{2}}\)

Таким образом, длина стороны ОВ равна длине стороны ОС, деленной на корень из 2.

Теперь рассмотрим треугольник АОВ. Согласно теореме косинусов, для нахождения длины стороны АВ можно использовать следующую формулу:

\(AB^2 = OB^2 + OA^2 — 2OB \cdot OA \cos 45°\)

Подставляя найденные ранее значения, получаем:

\(AB^2 = \left(\frac{OC}{\sqrt{2}}\right)^2 + \left(\frac{OC}{2}\right)^2 — 2 \cdot \frac{OC}{\sqrt{2}} \cdot \frac{OC}{2} \cdot \cos 45°\)
\(AB^2 = \frac{OC^2}{2} + \frac{OC^2}{4} — OC^2 \cdot \frac{1}{2\sqrt{2}} = \frac{OC^2}{2}\)
\(AB = \frac{OC}{\sqrt{2}}\)

Таким образом, треугольник АОВ является равнобедренным, с длиной сторон \(OA = AB = \frac{OC}{\sqrt{2}}\).

Прямые НО и СВ перпендикулярны к плоскости треугольника АВО, то есть они лежат в одной плоскости. Следовательно, угол между ними равен 90 градусам (\(\angle HOB = 90°\)), а угол между сторонами ОВ и СВ равен 45 градусам (\(\angle COB = 45°\)). Таким образом, искомый угол равен 45 градусам.