
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 756 Атанасян — Подробные Ответы
Проекция точки М на плоскость ромба ABCD совпадает с точкой О пересечения его диагоналей. Точка N — середина стороны ВС, \(AC=8\), \(DB= MO = 6\). Вычислите косинус угла между прямой MN и прямой: а) \(\vec{BC}\); б) \(\vec{DC}\); в) \(\vec{AC}\); г) \(\vec{DB}\).
Определим координаты:
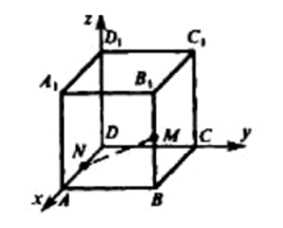
A \((a,0,0)\), \(A_1(a,0,a)\), B \((a,a,0)\), \(B_1(a,a,a)\), D \((0,0,0)\), M \((a,a,\frac{3a}{5})\), N \((\frac{3a}{5},0,0)\).
Вектор \(\overrightarrow{NM} = (a — \frac{3a}{5}, a — 0, \frac{3a}{5} — 0) = (\frac{2a}{5}, a, \frac{3a}{5})\),
\(\overrightarrow{DA} = (a,0,0)\).
\(\cos(\angle NMDA) = \left| \frac{\overrightarrow{NM} \cdot \overrightarrow{DA}}{|\overrightarrow{NM}| \cdot |\overrightarrow{DA}|} \right| = \left| \frac{\frac{2a}{5} \cdot a}{\sqrt{(\frac{2a}{5})^2 + a^2 + (\frac{3a}{5})^2} \cdot a} \right| = \left| \frac{\frac{2}{5} a^2}{a \sqrt{\frac{4}{25}a^2 + a^2 + \frac{9}{25}a^2}} \right| =\)
\(= \left| \frac{\frac{2}{5} a^2}{a^2 \sqrt{\frac{38}{25}}} \right| = \frac{2}{5} \cdot \frac{5}{\sqrt{38}} = \frac{2}{\sqrt{38}} \)
Ответ: \(\sin(\angle NM(DD_1C_1)) = \frac{2}{\sqrt{38}}\)
Для второго угла:
\(\overrightarrow{NM} = (\frac{2a}{5}, a, \frac{3a}{5})\),
\(\overrightarrow{AA_1} = (0, 0, a)\).
\(\cos(\angle NMAA_1) = \left| \frac{\frac{3a}{5} \cdot a}{|\overrightarrow{NM}| \cdot a} \right| = \left| \frac{\frac{3}{5} a^2}{a \cdot a \sqrt{\frac{38}{25}}} \right| = \frac{3}{5} \cdot \frac{5}{\sqrt{38}} = \frac{3}{\sqrt{38}} \)
Ответ: \(\sin(\angle NM(A_1B_1C_1)) = \frac{3}{\sqrt{38}}\)
Определим систему координат с началом в точке D. Для удобства обозначим длину ребра куба как \( a \).
Координаты нужных вершин:
A \((a,0,0)\), \(A_1(a,0,a)\), B \((a,a,0)\), \(B_1(a,a,a)\), D \((0,0,0)\), M \((a,a,\frac{3a}{5})\), N \((\frac{3a}{5},0,0)\).
Рассмотрим векторы:
\(\overrightarrow{NM} = (a — \frac{3a}{5}, a — 0, \frac{3a}{5} — 0) = (\frac{2a}{5}, a, \frac{3a}{5})\)
\(\overrightarrow{DA} = (a-0, 0-0, 0-0) = (a, 0, 0)\)
Вычислим скалярное произведение:
\(\overrightarrow{NM} \cdot \overrightarrow{DA} = \frac{2a}{5} \cdot a + a \cdot 0 + \frac{3a}{5} \cdot 0 = \frac{2a^2}{5}\)
Найдём длины векторов:
\(|\overrightarrow{NM}| = \sqrt{(\frac{2a}{5})^2 + a^2 + (\frac{3a}{5})^2} = \sqrt{\frac{4a^2}{25} + a^2 + \frac{9a^2}{25}} = \sqrt{\frac{4a^2 + 25a^2 + 9a^2}{25}} =\)
\(= \sqrt{\frac{38a^2}{25}} = a\frac{\sqrt{38}}{5}\)
\(|\overrightarrow{DA}| = \sqrt{a^2 + 0 + 0} = a\)
Воспользуемся формулой косинуса угла между векторами:
\(\cos \alpha = \left| \frac{\overrightarrow{NM} \cdot \overrightarrow{DA}}{|\overrightarrow{NM}| \cdot |\overrightarrow{DA}|} \right| = \left| \frac{\frac{2a^2}{5}}{a \cdot a\frac{\sqrt{38}}{5}} \right| = \left| \frac{2a^2}{5} \cdot \frac{5}{a^2 \sqrt{38}} \right| = \left| \frac{2}{\sqrt{38}} \right|\)
Следовательно, \(\sin(\angle NM(DD_1C_1)) = \cos(\angle NMDA) = \frac{2}{\sqrt{38}}\).
Теперь рассмотрим второй угол:
\(\overrightarrow{AA_1} = (a-a, 0-0, a-0) = (0, 0, a)\)
Скалярное произведение:
\(\overrightarrow{NM} \cdot \overrightarrow{AA_1} = \frac{2a}{5} \cdot 0 + a \cdot 0 + \frac{3a}{5} \cdot a = \frac{3a^2}{5}\)
Длина \(|\overrightarrow{AA_1}| = a\)
По формуле:
\(\cos \beta = \left| \frac{\overrightarrow{NM} \cdot \overrightarrow{AA_1}}{|\overrightarrow{NM}| \cdot |\overrightarrow{AA_1}|} \right| = \left| \frac{\frac{3a^2}{5}}{a \cdot a \frac{\sqrt{38}}{5}} \right| = \left| \frac{3a^2}{5} \cdot \frac{5}{a^2 \sqrt{38}} \right| = \left| \frac{3}{\sqrt{38}} \right|\)
Ответ: \(\sin(\angle NM(A_1B_1C_1)) = \cos(\angle NMAA_1) = \frac{3}{\sqrt{38}}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!