
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 754 Атанасян — Подробные Ответы
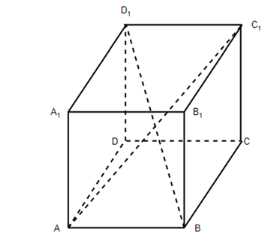
В параллелепипеде ABCDA1B1C1D1 \(\angle BAA_1 = \angle BAD = \angle DAA_1 = 60°\), \(AB = AA_1 = AD = 1\). Вычислите длины векторов \(\vec{AC_1}\) и \(\vec{BD_1}\).
Для вычислений используем формулы суммы и разности векторов.
а) \( \overrightarrow{AC_1} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1} \)
\( |\overrightarrow{AC_1}|^2 = ( \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1} )^2 = |\overrightarrow{AB}|^2 + |\overrightarrow{AD}|^2 + |\overrightarrow{AA_1}|^2 + \)
\(+2|\overrightarrow{AB}||\overrightarrow{AD}| \cos 60^\circ + 2|\overrightarrow{AB}||\overrightarrow{AA_1}| \cos 60^\circ + 2|\overrightarrow{AD}||\overrightarrow{AA_1}| \cos 60^\circ = \)
\(=3 + 1 + 2 + 3 \cdot 1 \cdot \frac{1}{2} = 6 \)
\( |\overrightarrow{AC_1}| = \sqrt{6} \)
б) \( \overrightarrow{BD_1} = \overrightarrow{AD} + \overrightarrow{AA_1} — \overrightarrow{AB} \)
\( |\overrightarrow{BD_1}|^2 = ( \overrightarrow{AD} + \overrightarrow{AA_1} — \overrightarrow{AB} )^2 = |\overrightarrow{AD}|^2 + |\overrightarrow{AA_1}|^2 + |\overrightarrow{AB}|^2 + \)
\(+2|\overrightarrow{AD}||\overrightarrow{AA_1}| \cos 60^\circ — 2|\overrightarrow{AD}||\overrightarrow{AB}| \cos 60^\circ — 2|\overrightarrow{AA_1}||\overrightarrow{AB}| \cos 60^\circ =\)
\(= 1 + 1 + 3 + 1 — 2 — 2 = 2 \)
\( |\overrightarrow{BD_1}| = \sqrt{2} \)
Для вычислений воспользуемся формулами суммы и разности векторов. Пусть длина ребра куба равна 1.
а) Рассмотрим вектор \( \overrightarrow{AC_1} \). Его можно разложить так: \( \overrightarrow{AC_1} = \overrightarrow{AC} + \overrightarrow{CC_1} \). Но \( \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} \), а \( \overrightarrow{BC} = \overrightarrow{BD} \). Тогда \( \overrightarrow{AC_1} = \overrightarrow{AB} + \overrightarrow{BD} + \overrightarrow{CC_1} \). Заметим, что \( \overrightarrow{BD} = \overrightarrow{AD} \), а \( \overrightarrow{CC_1} = \overrightarrow{AA_1} \). Итак, \( \overrightarrow{AC_1} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1} \).
Теперь найдём длину этого вектора. По формуле квадрата длины суммы трёх векторов:
\( |\overrightarrow{AC_1}|^2 = ( \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1} )^2 \).
Раскроем скобки:
\( |\overrightarrow{AC_1}|^2 = |\overrightarrow{AB}|^2 + |\overrightarrow{AD}|^2 + |\overrightarrow{AA_1}|^2 + 2 \overrightarrow{AB} \cdot \overrightarrow{AD} + 2 \overrightarrow{AB} \cdot \overrightarrow{AA_1} + 2 \overrightarrow{AD} \cdot \overrightarrow{AA_1} \).
Так как все векторы — рёбра куба и перпендикулярны друг другу, их длины равны 1, а скалярное произведение равно \( \cos 60^\circ \), так как угол между любыми двумя векторами из трёх возможных — 60° (по диагонали грани):
\( |\overrightarrow{AB}|^2 = 1 \), \( |\overrightarrow{AD}|^2 = 1 \), \( |\overrightarrow{AA_1}|^2 = 1 \).
Скалярные произведения:
\( \overrightarrow{AB} \cdot \overrightarrow{AD} = |\overrightarrow{AB}| \cdot |\overrightarrow{AD}| \cdot \cos 60^\circ = 1 \cdot 1 \cdot \frac{1}{2} = \frac{1}{2} \).
Аналогично для остальных пар:
\( \overrightarrow{AB} \cdot \overrightarrow{AA_1} = \frac{1}{2} \), \( \overrightarrow{AD} \cdot \overrightarrow{AA_1} = \frac{1}{2} \).
Подставляем в формулу:
\( |\overrightarrow{AC_1}|^2 = 1 + 1 + 1 + 2 \cdot \frac{1}{2} + 2 \cdot \frac{1}{2} + 2 \cdot \frac{1}{2} = 3 + 3 \cdot 1 = 6 \).
Значит,
\( |\overrightarrow{AC_1}| = \sqrt{6} \).
б) Теперь рассмотрим \( \overrightarrow{BD_1} \). Его можно разложить так: \( \overrightarrow{BD_1} = \overrightarrow{BD} + \overrightarrow{DD_1} \).
\( \overrightarrow{BD} = \overrightarrow{BA} + \overrightarrow{AD} \), а \( \overrightarrow{DD_1} = \overrightarrow{AA_1} \).
Тогда \( \overrightarrow{BD_1} = \overrightarrow{BA} + \overrightarrow{AD} + \overrightarrow{AA_1} \).
Но \( \overrightarrow{BA} = -\overrightarrow{AB} \), поэтому \( \overrightarrow{BD_1} = -\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1} \).
Запишем это как \( \overrightarrow{BD_1} = \overrightarrow{AD} + \overrightarrow{AA_1} — \overrightarrow{AB} \).
Вычислим длину:
\( |\overrightarrow{BD_1}|^2 = ( \overrightarrow{AD} + \overrightarrow{AA_1} — \overrightarrow{AB} )^2 \)
Раскрываем скобки:
\( |\overrightarrow{BD_1}|^2 = |\overrightarrow{AD}|^2 + |\overrightarrow{AA_1}|^2 + |\overrightarrow{AB}|^2 + 2 \overrightarrow{AD} \cdot \overrightarrow{AA_1} — 2 \overrightarrow{AD} \cdot \overrightarrow{AB} — 2 \overrightarrow{AA_1} \cdot \overrightarrow{AB} \).
Подставляем значения:
\( |\overrightarrow{AD}|^2 = 1 \), \( |\overrightarrow{AA_1}|^2 = 1 \), \( |\overrightarrow{AB}|^2 = 1 \),
\( 2 \overrightarrow{AD} \cdot \overrightarrow{AA_1} = 2 \cdot \frac{1}{2} = 1 \),
\( -2 \overrightarrow{AD} \cdot \overrightarrow{AB} = -2 \cdot \frac{1}{2} = -1 \),
\( -2 \overrightarrow{AA_1} \cdot \overrightarrow{AB} = -2 \cdot \frac{1}{2} = -1 \).
Тогда
\( |\overrightarrow{BD_1}|^2 = 1 + 1 + 1 + 1 — 1 — 1 = 2 \).
Следовательно,
\( |\overrightarrow{BD_1}| = \sqrt{2} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!