Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 751 Атанасян — Подробные Ответы
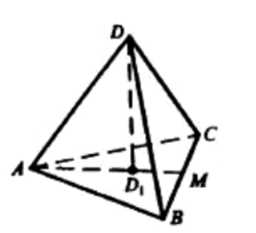
Все рёбра тетраэдра ABCD равны друг другу, D1 — проекция точки D на плоскость АВС. Перпендикулярны ли векторы: а) \(\vec{D_1B}\) и \(\vec{D_1D}\); б) \(\vec{DD_1}\) и \(\vec{BC}\); в) \(\vec{DA}\) и \(\vec{BC}\); г) \(\vec{D_1B}\) и \(\vec{DC}\)?
а) Вектор \(D_1D\) направляющий вектор прямой \(D_1D\), а вектор \(D_1B\) — направляющий вектор прямой \(D_1B\). Следовательно, вектор \(D_1B\) перпендикулярен вектору \(D_1D\).
б) Вектор \(DD_1\) также направляющий вектор прямой \(D_1D\), перпендикулярной плоскости \(ABC\). Таким образом, \(DD_1\) перпендикулярна \(BC\).
в) Векторы \(DA\) и \(BC\) направляющие векторы прямых \(DA\) и \(BC\) соответственно. Так как тетраэдр \(ABCD\) правильный, то вершина \(D\) проектируется в центр треугольника \(ABC\). Следовательно, \(DA\) перпендикулярна \(BC\).
г) Прямые \(DC\) и \(D_1B\) не перпендикулярны, так как они не перпендикулярны.
Согласно условию задачи, рассмотрим подробно каждый пункт:
а) Определение проекции прямой DD1 на плоскость ABC. Вектор D1D является направляющим вектором прямой D1D, а вектор D1B является направляющим вектором прямой D1B. Так как прямая DD1 перпендикулярна плоскости ABC, то вектор D1B перпендикулярен вектору D1D, то есть \(D_1B \perp D_1D\).
б) Вектор DD1 также является направляющим вектором прямой D1D, перпендикулярной плоскости ABC. Таким образом, DD1 перпендикулярна BC, так как BC является направляющим вектором прямой BC. Следовательно, \(DD_1 \perp BC\).
в) Векторы DA и BC являются направляющими векторами прямых DA и BC соответственно. Так как тетраэдр ABCD является правильным, вершина D проектируется в центр треугольника ABC. Следовательно, DA перпендикулярна BC, то есть \(DA \perp BC\).
г) Прямые DC и D1B не перпендикулярны, так как они не перпендикулярны. Если бы CD была перпендикулярна D1B, то по теореме, обратной к теореме о трех перпендикулярах, CD была бы перпендикулярна D1B. Однако, в данном случае, прямые DC и D1B не перпендикулярны, так как они содержат медианы правильного треугольника, которые не перпендикулярны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.