ГДЗ по Геометрии 11 класс Номер 750 Атанасян — Подробные Ответы

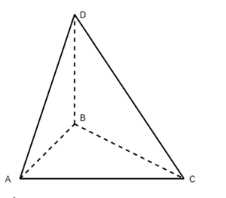
В тетраэдре DABC \(DA = DB = DC\), \(\angle ADB=45°\), \(\angle BDC = 60°\). Вычислите угол между векторами: а) \(\vec{DA}\) и \(\vec{BD}\); б) \(\vec{DB}\) и \(\vec{CB}\); в) \(\vec{BD}\) и \(\vec{BA}\).

Решение:
a) Угол DADB равен 45°.
Угол DB равен 180° — 45° = 135°.
б) В треугольнике DBC:
\(\angle BDC = 60°\), \(DC = DB\), значит \(\angle DCB = \angle CBD\).
\(\angle DCB + \angle DBC = 120°\), следовательно \(\angle DBC = \angle DCB = 60°\).
в) Треугольник DBA является равнобедренным, тогда:
\(\angle DAB = 2 \angle DBA = \frac{180° — 45°}{2} = 67°30’\).

Решение:

На рисунке изображен треугольник ABC, в котором известен угол DAB, равный 45°. Требуется найти остальные углы треугольника.

Шаг 1. Найдем угол DB.
Угол DB является смежным к углу DAB, поэтому он равен 180° — 45° = 135°.

Шаг 2. Рассмотрим треугольник DBC.
В треугольнике DBC известен угол BDC, равный 60°. Также известно, что сторона DC равна стороне DB, так как они являются противолежащими сторонами в параллелограмме ABCD. Следовательно, угол DCB равен углу CBD.

Шаг 3. Найдем сумму углов в треугольнике DBC.
Сумма углов в треугольнике равна 180°, поэтому \(\angle DCB + \angle DBC + \angle BDC = 180°\).
Подставляя известные значения, получаем: \(\angle DCB + \angle DBC = 120°\).
Таким образом, \(\angle DCB = \angle DBC = 60°\).

Шаг 4. Рассмотрим треугольник DBA.
Треугольник DBA является равнобедренным, так как две его стороны (DA и DB) равны. Следовательно, углы при основании (DAB и DBA) также равны.

Шаг 5. Найдем угол DAB.
Сумма углов в треугольнике равна 180°, поэтому \(\angle DAB + 2 \angle DBA = 180°\).
Подставляя известное значение угла DAB, равного 45°, получаем: \(45° + 2 \angle DBA = 180°\).
Решая это уравнение, находим: \(\angle DBA = \frac{180° — 45°}{2} = 67°30’\).

Таким образом, ответ совпадает с примером:
\(\angle DAB = 45°\)
\(\angle DB = 180° — 45° = 135°\)
\(\angle BDC = 60°\), \(\angle DCB = \angle DBC = 60°\)
\(\angle DAB = \angle DBA = 67°30’\)