
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 747 Атанасян — Подробные Ответы
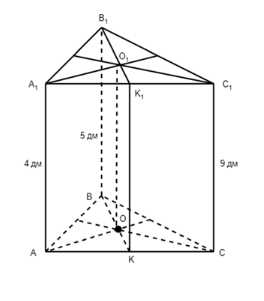
Вершины треугольника АВС расположены по одну сторону от плоскости \(\sigma\) и находятся от этой плоскости на расстояниях 4 дм, 5 дм и 9 дм. Найдите расстояние от точки пересечения медиан треугольника до плоскости \(\sigma\).
Из геометрии плоскости ABC и A1B1C1 следует, что они не параллельны, но расстояния между ними параллельны. Так как ВК и В1К1 являются медианами, то КК1 — средняя линия трапеции AA1C1C, длина которой равна \(КК_1 = \frac{AA_1 + CC_1}{2} = 6.5 \text{дм}\). Так как прямая ВВ1 параллельна АА1, а АА1 параллельна КК1, то ВВ1 параллельна КК1. Следовательно, ВККВВ1 — трапеция, а О и О1 — точки пересечения медиан. Известно, что медианы в точке пересечения делятся в соотношении 1:2. Поэтому трапеции ВОО1В1 и ВККВВ1 подобны, и длину искомого отрезка ОО1 можно вычислить как \(ОО_1 = ВВ_1 + \frac{КК_1 — ВВ_1}{3} = 6 \text{дм}\).
Рассмотрим данную задачу шаг за шагом:
1. Из условия задачи видно, что плоскости ABC и A1B1C1 не параллельны, так как расстояния между ними в разных точках различны. Однако, сами эти расстояния параллельны, так как они являются перпендикулярами, проведенными к одной из плоскостей.
2. Так как ВК и В1К1 являются медианами трапеции AA1C1C, то их средняя линия КК1 имеет длину \(КК_1 = \frac{AA_1 + CC_1}{2}\). Подставляя известные размеры, получаем \(КК_1 = \frac{4 + 9}{2} = 6.5 \text{дм}\).
3. Поскольку прямая ВВ1 параллельна прямой АА1, а прямая АА1 параллельна прямой КК1 (по свойству средней линии), то прямая ВВ1 также параллельна прямой КК1.
4. Таким образом, ВККВВ1 является трапецией. Точки О и О1 являются точками пересечения медиан этой трапеции.
5. Известно, что медианы трапеции делятся в точке пересечения в отношении 1:2. Следовательно, трапеции ВОО1В1 и ВККВВ1 подобны.
6. Используя это свойство подобия, можно вычислить длину искомого отрезка ОО1 по формуле \(ОО_1 = ВВ_1 + \frac{КК_1 — ВВ_1}{3}\). Подставляя известные значения, получаем \(ОО_1 = 4 + \frac{6.5 — 4}{3} = 6 \text{дм}\).
Таким образом, длина искомого отрезка ОО1 составляет \(6 \text{дм}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!