
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 727 Атанасян — Подробные Ответы
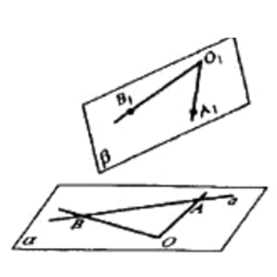
Докажите, что при движении: а) прямая отображается на прямую; б) плоскость отображается на плоскость.
a) Доказательство: точки A1, B1, C1 лежат на одной прямой. Согласно условию, \(AB=A_1B_1\), \(BC=B_1C_1\) и \(AC=A_1C_1\). Тогда \(A_1C_1=A_1B_1+B_1C_1\), что верно, если точки A1, B1, C1 лежат на одной прямой. В противном случае неравенство треугольника \(A_1C_1 < A_1B_1+B_1C_1\) будет нарушено. б) Проведем из точки O отрезки, пересекающие прямую в точках A и B. При движении O переходит в O1, A в A1, B в B1, соответственно \(OA=O_1A_1\), \(OB=O_1B_1\). Согласно аксиоме, через две пересекающиеся прямые проходит плоскость и притом только одна.
Рассмотрим задачу подробно:
a) Возьмем на прямой точки A, B, C. При движении они перейдут в точки A1, B1, C1 соответственно, причем \(AB=A_1B_1\), \(BC=B_1C_1\) и \(AC=A_1C_1\). Необходимо доказать, что точки A1, B1, C1 лежат на одной прямой.
Для этого рассмотрим расстояние между точками A1 и C1:
\(A_1C_1 = A_1B_1 + B_1C_1\)
Если точки A1, B1, C1 лежат на одной прямой, то это равенство будет выполняться. Если же они не лежат на одной прямой, то по неравенству треугольника будет \(A_1C_1 < A_1B_1 + B_1C_1\). Таким образом, доказательство того, что точки A1, B1, C1 лежат на одной прямой, сводится к проверке выполнения равенства \(A_1C_1 = A_1B_1 + B_1C_1\). б) Проведем на плоскости прямую и возьмем точку O, не принадлежащую этой прямой. Проведем из точки O отрезки, пересекающие прямую в точках A и B. При движении точка O перейдет в точку O1, A в A1, B в B1. Тогда \(OA=O_1A_1\) и \(OB=O_1B_1\). Согласно аксиоме, через две пересекающиеся прямые проходит плоскость и притом только одна. Таким образом, движение переводит прямую в прямую.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!