Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 724 Атанасян — Подробные Ответы
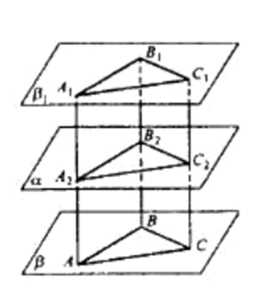
При зеркальной симметрии относительно плоскости \(\beta\) плоскость \(\beta\) отображается на плоскость \(\beta_1\). Докажите, что если: а) \(\beta \perp \alpha\), то \(\beta_1 \perp \alpha\); б) \(\beta \parallel \alpha\), то \(\beta_1\) совпадает с \(\beta\).
a) Выберем три точки A, B, C, не лежащие на одной прямой. Проведем AA2, BB2, CC2 перпендикулярно плоскости. Продолжим эти отрезки за точки A1, B1, C1, так что A2A1=AA2, B2B1=BB2, C2C1=CC2. AA1B1B — прямоугольник, так как AA1=BB1 и AA||BB1. Таким образом, A1B1||AB. BB1C1C — прямоугольник, т.к. BB1=CC1 и BB||BC. Тогда B1C1||BC. Плоскость β проходит через точки A1, B1, C1 и она единственная. Если две пересекающиеся прямые (BA и BC) одной плоскости параллельны двум прямым (B1A1 и B1C1) другой плоскости, то эти плоскости параллельны: β||γ.
б) Пусть α перпендикулярна β. Возьмём произвольную точку A на плоскости α и построим AO перпендикулярно плоскости α. Продолжим отрезок за точку O на расстояние OA=AO. Две плоскости взаимно перпендикулярны и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, тогда этот перпендикуляр весь лежит в этой плоскости, т.е. AO принадлежит β, следовательно и AA1 принадлежит β. Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая тоже принадлежит плоскости β. Тогда плоскость β либо отображается сама на себя, либо совпадает с α.
a) Выберем три точки A, B, C, не лежащие на одной прямой. Проведем отрезки AA2, BB2, CC2, перпендикулярные плоскости, на которой лежат точки A, B, C. Продолжим эти отрезки за точки A1, B1, C1 так, что A2A1=AA2, B2B1=BB2, C2C1=CC2. Таким образом, мы получили параллелограммы AA1B1B и BB1C1C. Так как AA1=BB1 и AA||BB1, то AA1B1B — прямоугольник. Аналогично, BB1C1C — прямоугольник, так как BB1=CC1 и BB||BC. Следовательно, B1C1||BC.
Плоскость β проходит через точки A1, B1, C1 и является единственной такой плоскостью. Если две пересекающиеся прямые (BA и BC) одной плоскости параллельны двум прямым (B1A1 и B1C1) другой плоскости, то эти плоскости параллельны: \(β||γ\).
б) Пусть плоскость α перпендикулярна плоскости β. Возьмём произвольную точку A на плоскости α и построим отрезок AO, перпендикулярный плоскости α. Продолжим отрезок за точку O на расстояние OA=AO. Две взаимно перпендикулярные плоскости, к одной из которых проведен перпендикуляр, имеющий общую точку с другой плоскостью, имеют то свойство, что этот перпендикуляр весь лежит в этой плоскости. Следовательно, AO принадлежит плоскости β, а значит и AA1 принадлежит β.
Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая также принадлежит плоскости β. Отсюда следует, что плоскость β либо отображается сама на себя, либо совпадает с плоскостью α.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.