
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 723 Атанасян — Подробные Ответы
При зеркальной симметрии прямая \(a\) отображается на прямую \(a_1\). Докажите, что прямые \(a\) и \(a_1\) лежат в одной плоскости
Если прямая а параллельна плоскости, то прямые ML и NK параллельны, так как MA=AL, NB=BK и NB=MA=BK=AL. Тогда ML=NK, и четырёхугольник MNKL — прямоугольник. По теореме, параллельные прямые лежат в одной плоскости.
Если прямая не параллельна плоскости, она пересекает её в некоторой точке. При симметрии эта точка переходит сама в себя, так как лежит в данной плоскости. Таким образом, прямая принадлежит и изначальной прямой, и симметричной, и они лежат в одной плоскости.
Дано: Прямая а параллельна плоскости α.
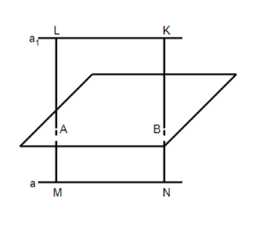
Шаг 1. Рассмотрим точки M, L, N и K на рисунке. Согласно условию, точки M и L, а также N и K симметричны относительно плоскости α.
Шаг 2. Так как точки M и L, N и K симметричны, то MA=AL и NB=BK.
Шаг 3. Если прямая а параллельна плоскости α, то прямые NB и MA, а также BK и AL параллельны. Следовательно, NB=MA=BK=AL.
Шаг 4. Поскольку NB=MA=BK=AL, две прямые ML и NK, перпендикулярные плоскости α, являются параллельными между собой. Таким образом, ML=NK.
Шаг 5. Так как ML=NK и четырёхугольник MNKL является прямоугольником, по теореме о параллельных прямых, ML и MN (или a и a1) лежат в одной плоскости.
Шаг 6. Если прямая а не параллельна плоскости α, она пересекает её в некоторой точке. При симметрии эта точка переходит сама в себя, так как лежит в данной плоскости.
Шаг 7. Таким образом, прямая принадлежит и изначальной прямой а, и симметричной прямой, и они лежат в одной плоскости.
Вывод: Независимо от того, параллельна ли прямая а плоскости α или нет, прямые, перпендикулярные этой плоскости, лежат в одной плоскости.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!