
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 722 Атанасян — Подробные Ответы
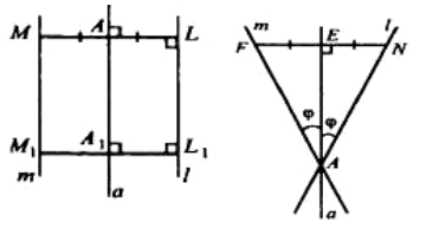
Докажите, что при осевой симметрии: а) прямая, параллельная оси, отображается на прямую, параллельную оси; б) прямая, образующая с осью угол \(\varphi\), отображается на прямую, также образующую с осью угол \(\varphi\)
a) Поскольку ML=M1L1 и ML перпендикулярна L1, то M1L1 также перпендикулярна L1, следовательно, четырёхугольник LMM1L1 является прямоугольником.
б) Если прямая а не параллельна L, то она пересекается с L в некоторой точке А. Проведём перпендикуляр NE к прямой а и продолжим его за точку Е на расстояние EF=NE. Через точку F проведём прямую FA. В треугольниках AEF и AEN, NE=EF и AE — общий катет, следовательно, угол AEF равен углу AEN, то есть \(\phi\). Таким образом, прямая m образует угол \(\phi\) с осью симметрии.
a) Рассмотрим первый случай. Из условия следует, что ML=M1L1 и ML перпендикулярна L1. Это означает, что M1L1 также перпендикулярна L1. Таким образом, четырёхугольник LMM1L1 является прямоугольником, поскольку противоположные стороны параллельны и перпендикулярны. Следовательно, ММ||L1L, и \(m=\frac{1}{m}\), что и требовалось доказать.
б) Рассмотрим второй случай. Если прямая а не параллельна L, то она пересекается с L в некоторой точке А. Выберем на прямой L произвольную точку N и проведём перпендикуляр NE к прямой а. Продолжим отрезок NE за точку Е на расстояние EF=NE. Через точку F проведём прямую FA. В треугольниках AEF и AEN, NE=EF и AE — общий катет, следовательно, угол AEF равен углу AEN, то есть \(\phi\). Таким образом, прямая m образует угол \(\phi\) с осью симметрии, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!