
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 721 Атанасян — Подробные Ответы
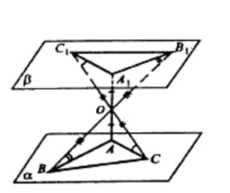
Докажите, что при центральной симметрии: а) плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость; б) плоскость, проходящая через центр симметрии, отображается на себя.
1. Выберем на плоскости точку С, проведем отрезок СО и продолжим его за точку О на расстояние \(OC_1=OC\).
2. Выберем на плоскости точку А, проведем отрезок АО и продолжим его за точку О на расстояние \(OA_1=OA\).
3. Выберем на плоскости точку В, проведем отрезок ВО и продолжим его за точку О на расстояние \(OB_1=OB\).
4. Через точки \(A_1, B_1, C_1\) проведем плоскость.
Доказательство:
Рассмотрим треугольники \(OAC\) и \(O_1A_1C_1\). Они равны, так как \(OA_1=OA\), \(OC_1=OC\) и углы \(AOC\) и \(A_1OC_1\) равны.
По признаку параллельности прямых \(A_1C\) параллельна \(AC\).
Аналогично доказывается, что \(A_1B_1=AB\).
По признаку параллельности плоскостей, плоскости \(ABC\) и \(A_1B_1C_1\) равны.
Если точка \(O\) принадлежит некоторой плоскости, то для любой точки \(A\) с этой плоскости прямая \(OA\) также будет принадлежать данной плоскости. Соответственно, любая точка этой прямой, в том числе и симметричная точка \(A_1\), принадлежит этой плоскости.
Аналогичные рассуждения проводим для пар точек \(B+B_1\) и \(C+C_1\). Через три точки \(A_1, B_1, C_1\) можно провести единственную плоскость, следовательно, она совпадает с исходной.
Построение:
1. Выберем на плоскости точку С. Проведем отрезок СО и продолжим его за точку О на расстояние \(OC_1=OC\).
2. Выберем на плоскости точку А. Проведем отрезок АО и продолжим его за точку О на расстояние \(OA_1=OA\).
3. Выберем на плоскости точку В. Проведем отрезок ВО и продолжим его за точку О на расстояние \(OB_1=OB\).
4. Через точки \(A_1, B_1, C_1\) проведем плоскость. Такая плоскость единственна.
Доказательство:
Рассмотрим треугольники \(OAC\) и \(O_1A_1C_1\). Очевидно, что они равны, так как \(OA_1=OA\), \(OC_1=OC\) и углы \(AOC\) и \(A_1OC_1\) равны.
По признаку параллельности прямых, прямая \(A_1C\) параллельна прямой \(AC\). Аналогично доказывается, что \(A_1B_1=AB\).
По признаку параллельности плоскостей, плоскости \(ABC\) и \(A_1B_1C_1\) равны, что и требовалось доказать.
Дополнительное обоснование:
Если точка \(O\) принадлежит некоторой плоскости, то для любой точки \(A\) этой плоскости прямая \(OA\) также будет принадлежать данной плоскости. Соответственно, любая точка этой прямой, в том числе и симметричная точка \(A_1\), принадлежит этой плоскости.
Аналогичные рассуждения проводим для пар точек \(B+B_1\) и \(C+C_1\). Через три точки \(A_1, B_1, C_1\) можно провести единственную плоскость, следовательно, она совпадает с исходной.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!