
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 720 Атанасян — Подробные Ответы
Докажите, что при центральной симметрии: а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую; б) прямая, проходящая через центр симметрии, отображается на себя
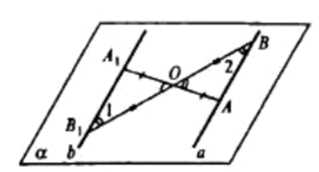
a) Через центр симметрии O и прямую a можно провести единственную плоскость. Точка A принадлежит прямой, построим отрезок OA. Продолжим OA за точку O на расстояние OA1=AO, получим симметричную точку A1. Аналогично построим точку B1, симметричную B. Тогда треугольники AOB и A1OB1 равны, как вертикальные, и углы B1BA и BB1A1 равны.
б) Точка A принадлежит прямой. Симметричная ей точка A1 также принадлежит этой прямой. Следовательно, любая точка прямой и ее симметричная относительно центра O лежат на прямой, т.е. прямая переходит сама в себя при условии, что проходит через центр симметрии.
Задача состоит в том, чтобы показать, как через центр симметрии O и прямую a можно провести единственную плоскость, а также как симметричная точка A1 принадлежит той же прямой, что и точка A.
Рассмотрим первую часть задачи:
1) Пусть O — центр симметрии, а — прямая, а — плоскость, проведенная через O и a.
2) Возьмем точку A, принадлежащую прямой a. Построим отрезок OA.
3) Продолжим OA за точку O на расстояние OA1 = AO. Получим симметричную точку A1.
4) Аналогично построим точку B1, симметричную B.
5) Треугольники AOB и A1OB1 равны, как вертикальные. Следовательно, углы B1BA и BB1A1 равны.
Рассмотрим вторую часть задачи:
1) Пусть точка A принадлежит прямой.
2) Симметричная ей точка A1 также принадлежит этой прямой.
3) Следовательно, любая точка прямой a и ее симметричная относительно центра O лежат на прямой a.
4) Таким образом, прямая a переходит сама в себя при условии, что проходит через центр симметрии O.
Ключевые моменты:
— Через центр симметрии O и прямую a можно провести единственную плоскость.
— Симметричная точка A1 принадлежит той же прямой a, что и точка A.
— Любая точка прямой a и ее симметричная относительно центра O лежат на прямой a.
— Прямая a переходит сама в себя при условии, что проходит через центр симметрии O.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!