ГДЗ по Геометрии 11 класс Номер 718 Атанасян — Подробные Ответы

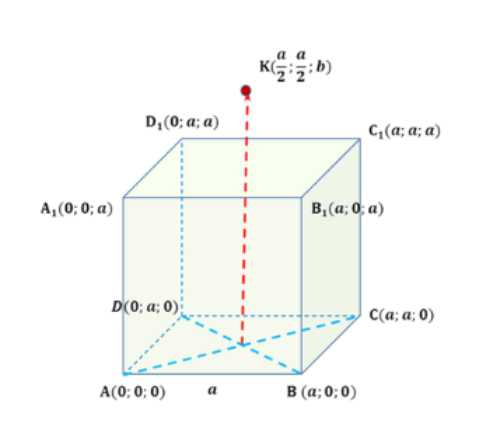
Проекция точки К на плоскость квадрата ABCD совпадает с центром этого квадрата. Докажите, что угол между прямыми АК и BD равен 90°.

Решение:
Введем ПСК с центром в точке А(0; 0; 0). Координаты вершин квадрата и куба известны. Найдем координату \(z\) точки К, неизвестную из условия.
Вычислим скалярное произведение векторов \(\vec{AK}\) и \(\vec{BD}\):
\(\vec{AK} \cdot \vec{BD} = \left[\frac{a}{2}, \frac{a}{2}, b\right] \cdot \left[-a, a, 0\right] = -\frac{a^2}{2} + \frac{a^2}{2} + 0 = 0\)
Таким образом, угол между векторами \(\vec{AK}\) и \(\vec{BD}\) равен 90°, что и требовалось доказать.

Решение:

Дано: ABCD — квадрат со стороной \(a\), точка К проецируется в центр квадрата. Необходимо доказать, что угол между векторами \(\vec{AK}\) и \(\vec{BD}\) равен 90°.

Для решения данной задачи будем использовать прямоугольную систему координат (ПСК) с центром в точке \(A(0; 0; 0)\). Это позволит нам определить координаты вершин квадрата и куба.

Координаты вершин квадрата:
\(A(0; 0; 0)\), \(B(a; 0; 0)\), \(C(a; a; 0)\), \(D(0; a; 0)\)

Координаты вершин куба:
\(A(0; 0; 0)\), \(B(a; 0; 0)\), \(C(a; a; 0)\), \(D(0; a; 0)\)
\(A_1(0; 0; a)\), \(B_1(a; 0; a)\), \(C_1(a; a; a)\), \(D_1(0; a; a)\)

Для нахождения координаты \(z\) точки \(K\) воспользуемся условием задачи, согласно которому точка \(K\) проецируется в центр квадрата. Обозначим эту координату как \(b\).

Теперь вычислим скалярное произведение векторов \(\vec{AK}\) и \(\vec{BD}\):
\(\vec{AK} = \left(\frac{a}{2}, \frac{a}{2}, b\right)\)
\(\vec{BD} = (-a, a, 0)\)

\(\vec{AK} \cdot \vec{BD} = \left(\frac{a}{2}\right)(-a) + \left(\frac{a}{2}\right)(a) + b(0) = -\frac{a^2}{2} + \frac{a^2}{2} + 0 = 0\)

Таким образом, скалярное произведение векторов \(\vec{AK}\) и \(\vec{BD}\) равно 0, что означает, что угол между ними равен 90°, что и требовалось доказать.