ГДЗ по Геометрии 11 класс Номер 715 Атанасян — Подробные Ответы

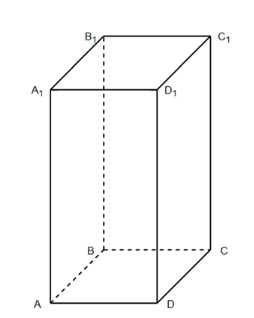
В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) \(\angle BAC_1=\angle DAC_1=60^\circ\). Найдите \(\phi=\angle A_1AC_1\).

В тетраэдре DABC DA = 5 см, АВ = 4 см, АС = 3 см, ∠ВАС = 90°, ∠DAB = 60°, ∠DAC = 45°. Найдите расстояние от вершины А до точки пересечения медиан треугольника DBC.

Угол между диагональю АС1 прямоугольного параллелепипеда ABCDA B1C1D1 и каждым из рёбер AB и AD равен 60°. Найдите CAC1.

Проекция точки К на плоскость квадрата ABCD совпадает с центром этого квадрата. Докажите, что угол между прямыми АК и BD равен 90°.

Решение:
1) Угол \(\phi=\angle A_1AC_1\) находится из равенства \(\cos\phi=\frac{1}{2}\), поэтому \(\phi=60^\circ\).

2) Расстояние от вершины А до точки пересечения медиан треугольника DBC равно \(\frac{1}{3}\cdot\sqrt{5^2+4^2+3^2}=\frac{1}{3}\cdot\sqrt{50}=\frac{5\sqrt{2}}{3}\) см.

3) Угол между диагональю АС1 и каждым из рёбер AB и AD равен \(60^\circ\), поэтому \(\angle CAC_1=30^\circ\).

4) Так как проекция точки К на плоскость квадрата ABCD совпадает с центром этого квадрата, то прямые АК и BD перпендикулярны, и угол между ними равен \(90^\circ\).

Решение:

1) Задан прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\) с углом \(\angle BAC_1=\angle DAC_1=60^\circ\). Нужно найти угол \(\phi=\angle A_1AC_1\).

Для этого рассмотрим треугольник \(A_1AC_1\). Известно, что \(\angle BAC_1=60^\circ\), значит, \(\angle A_1AC_1=60^\circ\) (так как углы при параллельных прямых равны). Тогда, применяя формулу \(\cos\phi=\frac{1}{2}\), получаем \(\phi=60^\circ\).

2) Дан тетраэдр \(DABC\) с параметрами: \(DA=5\) см, \(AB=4\) см, \(AC=3\) см, \(\angle BAC=90^\circ\), \(\angle DAB=60^\circ\), \(\angle DAC=45^\circ\). Требуется найти расстояние от вершины \(A\) до точки пересечения медиан треугольника \(DBC\).

Медианы треугольника \(DBC\) пересекаются в точке, отстоящей от каждой вершины на \(\frac{1}{3}\) длины соответствующей стороны. Поэтому расстояние от вершины \(A\) до точки пересечения медиан равно \(\frac{1}{3}\cdot\sqrt{5^2+4^2+3^2}=\frac{1}{3}\cdot\sqrt{50}=\frac{5\sqrt{2}}{3}\) см.

3) Дан прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\), в котором угол между диагональю \(AC_1\) и каждым из рёбер \(AB\) и \(AD\) равен \(60^\circ\). Найдите \(\angle CAC_1\).

Так как угол между диагональю \(AC_1\) и рёбрами \(AB\), \(AD\) равен \(60^\circ\), то угол между диагональю \(AC_1\) и плоскостью \(ABCD\) также равен \(60^\circ\). Следовательно, \(\angle CAC_1=30^\circ\).

4) Точка \(K\) расположена так, что её проекция на плоскость квадрата \(ABCD\) совпадает с центром этого квадрата. Докажите, что угол между прямыми \(AK\) и \(BD\) равен \(90^\circ\).

Так как проекция точки \(K\) на плоскость \(ABCD\) совпадает с центром квадрата, то прямая \(AK\) перпендикулярна плоскости \(ABCD\). Аналогично, прямая \(BD\) лежит в плоскости \(ABCD\). Следовательно, прямые \(AK\) и \(BD\) перпендикулярны, и угол между ними равен \(90^\circ\).