Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 714 Атанасян — Подробные Ответы
Лучи \(OA\), \(OB\) и \(OC\) образуют три прямых угла \(AOB\), \(AOC\) и \(BOC\). Найдите угол между биссектрисами углов \(COA\) и \(AOB\).
Решение:
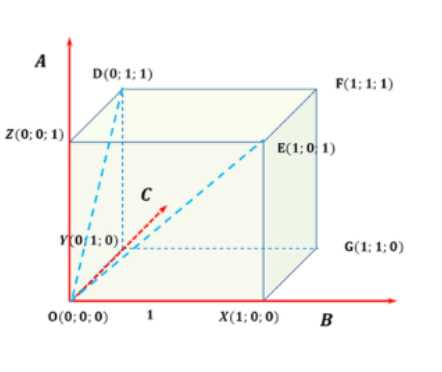
Введем прямоугольную систему координат с центром в точке \(O(0, 0, 0)\) и осями, направленными вдоль лучей \(OA\), \(OB\) и \(OC\). Построим единичный куб на перпендикулярных осях и проведем биссектрисы углов \(AOB\) и \(AOC\) как диагонали граней куба. Координаты точек \(D(0, 1, 1)\) и \(E(1, 0, 1)\) известны. Используя формулу косинуса угла между векторами \(\cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\), получаем \(\cos(OD, OE) = \frac{0 \cdot 1 + 1 \cdot 0 + 1 \cdot 1}{\sqrt{0^2 + 1^2 + 1^2} \sqrt{1^2 + 0^2 + 1^2}} = \frac{1}{2}\). Следовательно, угол между биссектрисами углов \(AOB\) и \(AOC\) равен \(60^\circ\).
Решение:
Дано:
— Лучи \(OA\), \(OB\) и \(OC\) образуют три прямых угла \(AOB\), \(AOC\) и \(BOC\).
— \(LAOD = LDOC\) и \(LAOE = LEOD\), то есть углы \(AOD\) и \(AOE\) равны углам \(DOC\) и \(EOD\) соответственно.
Для решения задачи выполним следующие шаги:
1. Введем прямоугольную систему координат с центром в точке \(O(0, 0, 0)\) и осями, направленными вдоль лучей \(OA\), \(OB\) и \(OC\).
2. Построим единичный куб на перпендикулярных осях.
3. Проведем биссектрисы углов \(AOB\) и \(AOC\) как диагонали граней куба.
4. Найдем координаты точек \(D(0, 1, 1)\) и \(E(1, 0, 1)\), лежащих на биссектрисах.
5. Используем формулу косинуса угла между векторами \(\cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\) для вычисления угла между векторами \(\vec{OD}\) и \(\vec{OE}\).
6. Подставляя координаты точек \(D\) и \(E\) в формулу, получаем \(\cos(OD, OE) = \frac{0 \cdot 1 + 1 \cdot 0 + 1 \cdot 1}{\sqrt{0^2 + 1^2 + 1^2} \sqrt{1^2 + 0^2 + 1^2}} = \frac{1}{2}\).
7. Таким образом, угол между биссектрисами углов \(AOB\) и \(AOC\) равен \(60^\circ\).
Ответ: Угол между биссектрисами углов \(AOB\) и \(AOC\) равен \(60^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.