Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 696 Атанасян — Подробные Ответы
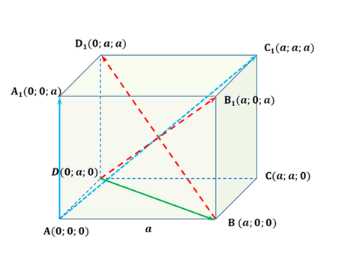
Дан куб ABCDA1B1C1D1. Вычислите косинус угла между векторами: а) АА1 и АС1; б) BD1 и DB1; в) DB и AC1.
а) cos(AA1, AC1) = \(\frac{0 \cdot a + 0 \cdot a + a \cdot a}{a \cdot a \cdot \sqrt{3}}\) = \(\frac{1}{\sqrt{3}}\)
б) cos(BD1, DB1) = \(\frac{-a \cdot a — a \cdot a + a \cdot a}{a \cdot \sqrt{3} \cdot a \cdot \sqrt{3}}\) = \(-\frac{1}{3}\)
в) cos(DB, AC1) = \(\frac{a \cdot 0 — 0 \cdot a + 0 \cdot a}{a \cdot \sqrt{2} \cdot a \cdot \sqrt{3}}\) = 0
Дано: куб ABCDA1B1C1D1, где AB = a. Требуется найти косинусы углов между следующими векторами:
а) АА1 и АС1
Для вычисления косинуса угла между векторами АА1 и АС1 используем формулу:
\(cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\)
Координаты точек:
А(0, 0, 0), А1(0, 0, a), С(a, a, a), С1(a, a, a)
Вектор АА1 = (0, 0, a)
Вектор АС1 = (a, a, a)
Находим длины векторов:
\(|АА1| = \sqrt{0^2 + 0^2 + a^2} = a\)
\(|АС1| = \sqrt{a^2 + a^2 + a^2} = a\sqrt{3}\)
Находим скалярное произведение векторов:
\(\vec{AA1} \cdot \vec{AC1} = 0 \cdot a + 0 \cdot a + a \cdot a = a^2\)
Подставляем в формулу:
\(cos(\vec{AA1}, \vec{AC1}) = \frac{a^2}{a \cdot a\sqrt{3}} = \frac{1}{\sqrt{3}}\)
б) BD1 и DB1
Для вычисления косинуса угла между векторами BD1 и DB1 используем формулу:
\(cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\)
Координаты точек:
B(a, 0, 0), D(0, a, 0), B1(a, 0, a), D1(0, a, a)
Вектор BD1 = (a, 0, a)
Вектор DB1 = (-a, a, a)
Находим длины векторов:
\(|BD1| = \sqrt{a^2 + 0^2 + a^2} = a\sqrt{2}\)
\(|DB1| = \sqrt{a^2 + a^2 + a^2} = a\sqrt{3}\)
Находим скалярное произведение векторов:
\(\vec{BD1} \cdot \vec{DB1} = -a \cdot a + 0 \cdot a + a \cdot a = -a^2\)
Подставляем в формулу:
\(cos(\vec{BD1}, \vec{DB1}) = \frac{-a^2}{a\sqrt{2} \cdot a\sqrt{3}} = -\frac{1}{3}\)
в) DB и AC1
Для вычисления косинуса угла между векторами DB и AC1 используем формулу:
\(cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\)
Координаты точек:
D(0, a, 0), B(a, 0, 0), C(a, a, a), C1(a, a, a)
Вектор DB = (a, -a, 0)
Вектор AC1 = (a, a, a)
Находим длины векторов:
\(|DB| = \sqrt{a^2 + a^2 + 0^2} = a\sqrt{2}\)
\(|AC1| = \sqrt{a^2 + a^2 + a^2} = a\sqrt{3}\)
Находим скалярное произведение векторов:
\(\vec{DB} \cdot \vec{AC1} = a \cdot a — a \cdot a + 0 \cdot a = 0\)
Подставляем в формулу:
\(cos(\vec{DB}, \vec{AC1}) = \frac{0}{a\sqrt{2} \cdot a\sqrt{3}} = 0\)
Таким образом, получаем:
а) cos(АА1, АС1) = 1/√3
б) cos(BD1, DB1) = -1/3
в) cos(DB, AC1) = 0
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.