
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 682 Атанасян — Подробные Ответы
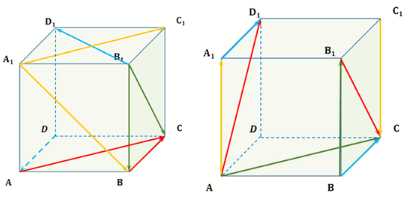
Дан куб ABCDA1B1C1D1. Найдите угол между векторами: а) \(\vec{B_1B}\) и \(\vec{B_1C}\); б) \(\vec{DA}\) и \(\vec{B_1D_1}\); в) \(\vec{A_1C_1}\) и \(\vec{A_1B}\); г) \(\vec{BC}\) и \(\vec{AC}\); д) \(\vec{BB_1}\) и \(\vec{AC}\); е) \(\vec{B_1C}\) и \(\vec{AD_1}\); ж) \(\vec{A_1D_1}\) и \(\vec{BC}\); з) \(\vec{AA_1}\) и \(\vec{C_1C}\).
а) \(\angle \text{B}_1\text{B}\text{B}_1\text{C} = 45^\circ\) (угол в равнобедренном прямоугольном треугольнике)
б) \(\angle \text{DA}\text{B}_1\text{D}_1 = 180^\circ — \angle \text{A}_1\text{D}_1\text{B}_1 = 135^\circ\)
в) \(\angle \text{A}_1\text{C}_1\text{A}_1\text{B} = 60^\circ\) (угол в равностороннем треугольнике)
г) \(\angle \text{BC}\text{AC} = \angle \text{AD}\text{AC} = 45^\circ\) (см. п. )
д) \(\angle \text{BB}_1\text{AC} = \angle \text{AA}_1\text{AC} = 90^\circ\) (угол в прямоугольнике)
е) \(\angle \text{B}_1\text{C}\text{AD}_1 = \angle \text{A}_1\text{D}\text{AD}_1 = 90^\circ\) (диагонали квадрата перпендикулярны)
ж) \(\angle \text{A}_1\text{D}_1\text{BC} = \angle \text{BC}\text{BC} = 0^\circ\) (угол между одинаковыми векторами)
з) \(\angle \text{AA}_1\text{C}_1\text{C} = \angle \text{C}_1\text{C}\text{C}_1\text{C} = 180^\circ\) (угол между противоположными векторами)
Для решения данной задачи мы будем использовать свойства куба и геометрические соотношения между векторами.
а) Для нахождения угла между векторами \(\text{B}_1\text{B}\) и \(\text{B}_1\text{C}\) мы можем использовать тот факт, что в прямоугольном треугольнике с гипотенузой \(\text{B}_1\text{C}\) и катетом \(\text{B}_1\text{B}\) угол между ними будет равен \(45^\circ\).
б) Угол между векторами \(\text{DA}\) и \(\text{B}_1\text{D}_1\) можно найти, используя свойство куба. Так как вектор \(\text{DA}\) противоположен вектору \(\text{B}_1\text{D}_1\), то угол между ними равен \(180^\circ\). Затем мы вычитаем угол \(\angle \text{A}_1\text{D}_1\text{B}_1\), который равен \(45^\circ\), чтобы получить итоговый угол \(180^\circ — 45^\circ = 135^\circ\).
в) Угол между векторами \(\text{A}_1\text{C}_1\) и \(\text{A}_1\text{B}\) равен \(60^\circ\), так как в равностороннем треугольнике все углы равны \(60^\circ\).
г) Угол между векторами \(\text{BC}\) и \(\text{AC}\) равен \(45^\circ\), так как эти векторы образуют диагональ квадрата.
д) Угол между векторами \(\text{BB}_1\) и \(\text{AC}\) равен \(90^\circ\), так как они образуют прямой угол в прямоугольнике.
е) Угол между векторами \(\text{B}_1\text{C}\) и \(\text{AD}_1\) равен \(90^\circ\), так как диагонали квадрата перпендикулярны.
ж) Угол между векторами \(\text{A}_1\text{D}_1\) и \(\text{BC}\) равен \(0^\circ\), так как эти векторы совпадают по направлению.
з) Угол между векторами \(\text{AA}_1\) и \(\text{C}_1\text{C}\) равен \(180^\circ\), так как эти векторы противоположны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!