ГДЗ по Геометрии 11 класс Номер 677 Атанасян — Подробные Ответы

Отрезок CD длины m перпендикулярен к плоскости прямоугольного треугольника АВС с катетами AC= b и ВС= a. Введите подходящую систему координат и с помощью формулы расстояния между двумя точками найдите расстояние от точки D до середины гипотенузы этого треугольника.

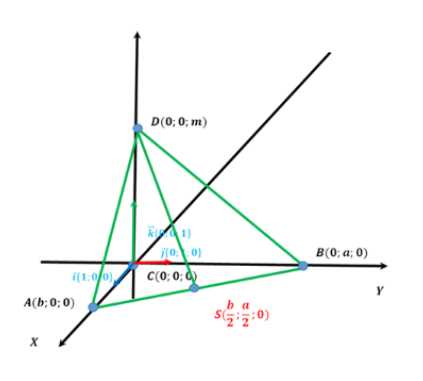
Введем прямоугольную систему координат, где точка С(0, 0, 0), A(b, 0, 0), B(0, a, 0) и D(0, 0, m). Тогда координаты середины отрезка AB равны \(\left(\frac{b}{2}, \frac{a}{2}, 0\right)\). Для нахождения расстояния от точки D до середины гипотенузы AB воспользуемся формулой расстояния между двумя точками:
\(|DS| = \sqrt{(0 — \frac{b}{2})^2 + (0 — \frac{a}{2})^2 + (m — 0)^2} = \sqrt{\frac{b^2}{4} + \frac{a^2}{4} + m^2}\)

Дано:
— Прямоугольный треугольник ABC с катетами AC = b и BC = a
— Точка D расположена на перпендикуляре, опущенном из вершины C на гипотенузу AB
— Длина отрезка CD равна m

Для решения задачи:

1. Введем прямоугольную систему координат, расположив начало координат в точке C(0, 0, 0).
2. Координаты вершин треугольника ABC будут:
— A(b, 0, 0)
— B(0, a, 0)
— C(0, 0, 0)
3. Координаты точки D будут: D(0, 0, m)
4. Чтобы найти координаты середины гипотенузы AB, воспользуемся формулой для вычисления координат середины отрезка:
\(\left(\frac{x_A + x_B}{2}, \frac{y_A + y_B}{2}, \frac{z_A + z_B}{2}\right) = \left(\frac{b}{2}, \frac{a}{2}, 0\right)\)
5. Для нахождения расстояния от точки D до середины гипотенузы AB, применим формулу расстояния между двумя точками:
\(|DS| = \sqrt{(x_D — x_S)^2 + (y_D — y_S)^2 + (z_D — z_S)^2}\)
Подставляя известные координаты, получаем:
\(|DS| = \sqrt{\left(0 — \frac{b}{2}\right)^2 + \left(0 — \frac{a}{2}\right)^2 + (m — 0)^2} = \sqrt{\frac{b^2}{4} + \frac{a^2}{4} + m^2}\)

Ответ: \(|DS| = \sqrt{\frac{b^2}{4} + \frac{a^2}{4} + m^2}\)