
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 676 Атанасян — Подробные Ответы
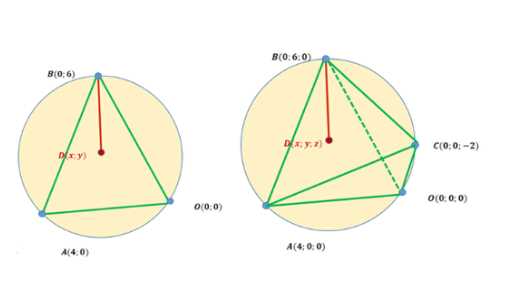
Даны точки О (0; 0; 0), А (4; 0; 0), В (0; 6; 0), С (0; 0; -2). Найдите: а) координаты центра и радиус окружности, описанной около треугольника ДОВ; б) координаты точки, равноудаленной от вершин тетраэдра ОАВС.
Решение задачи:
а) Определение координат центра и радиуса окружности, описанной около тетраэдра ΔABC.
Заметим, что координаты вершин тетраэдра ΔABC имеют нулевую аппликату (z-координату), то есть лежат в плоскости Oxy. Следовательно, данная стереометрическая задача может быть решена в плоскости.
Пусть точка D(x, y) является центром описанной окружности. Тогда для нахождения её координат можно воспользоваться формулой для расстояния между двумя точками:
\(AB = \sqrt{(x_B — x_A)^2 + (y_B — y_A)^2}\)
Для точек A(4, 0, 0), B(0, 6, 0) и C(0, 0, -2) имеем:
\(OD = AD = BD = \sqrt{(x — 0)^2 + (y — 0)^2} = \sqrt{x^2 + y^2}\)
\(AD = \sqrt{(x — 4)^2 + (y — 0)^2} = \sqrt{x^2 — 8x + 16 + y^2}\)
\(BD = \sqrt{(x — 0)^2 + (y — 6)^2} = \sqrt{x^2 + y^2 — 12y + 36}\)
Поскольку OD = AD = BD, можно составить уравнение:
\(x^2 + y^2 = x^2 — 8x + 16 + y^2 = x^2 + y^2 — 12y + 36\)
Решая это уравнение, получаем:
\(x = 2, y = 3\)
Таким образом, координаты центра описанной окружности: D(2, 3, 0).
Радиус окружности равен:
\(R_{ΔABC} = |OD| = \sqrt{x^2 + y^2} = \sqrt{2^2 + 3^2} = \sqrt{13}\)
б) Определение координат точки, равноудалённой от вершин тетраэдра ΟABC.
Пусть точка D(x, y, z) является искомой точкой, равноудалённой от вершин тетраэдра ΟABC.
Тогда для нахождения её координат можно воспользоваться формулой для расстояния между двумя точками:
\(AB = \sqrt{(x_B — x_A)^2 + (y_B — y_A)^2 + (z_B — z_A)^2}\)
Для точек A(4, 0, 0), B(0, 6, 0), C(0, 0, -2) и D(x, y, z) имеем:
\(OD = AD = BD = CD = \sqrt{x^2 + y^2 + z^2}\)
\(AD = \sqrt{(x — 4)^2 + (y — 0)^2 + (z — 0)^2} = \sqrt{x^2 — 8x + 16 + y^2 + z^2}\)
\(BD = \sqrt{(x — 0)^2 + (y — 6)^2 + (z — 0)^2} = \sqrt{x^2 + y^2 — 12y + 36 + z^2}\)
\(CD = \sqrt{(x — 0)^2 + (y — 0)^2 + (z + 2)^2} = \sqrt{x^2 + y^2 + 4z + 4}\)
Поскольку OD = AD = BD = CD, можно составить уравнение:
\(x^2 + y^2 + z^2 = x^2 — 8x + 16 + y^2 + z^2 = x^2 + y^2 — 12y + 36 + z^2 = \)
\(=x^2 + y^2 + 4z + 4\)
Решая это уравнение, получаем:
\(x = 2, y = 3, z = -1\)
Таким образом, координаты точки, равноудалённой от вершин тетраэдра ΟABC: D(2, 3, -1).
Для решения задачи о нахождении координат центра и радиуса окружности, описанной около тетраэдра ΔABC, а также координат точки, равноудалённой от вершин тетраэдра ΟABC, будем следовать следующим шагам.
Сначала определим координаты вершин тетраэдра. Пусть точки A(4, 0, 0), B(0, 6, 0) и C(0, 0, -2). Мы будем работать в плоскости Oxy, так как z-координаты вершин равны нулю.
Для нахождения координат центра описанной окружности D(x, y) будем использовать равенство расстояний от точки D до вершин A и B. Расстояние между двумя точками в плоскости определяется формулой:
\(AB = \sqrt{(x_B — x_A)^2 + (y_B — y_A)^2}\)
Сначала найдем расстояния:
\(OD = AD = BD\)
Где:
\(OD = \sqrt{x^2 + y^2}\)
\(AD = \sqrt{(x — 4)^2 + (y — 0)^2} = \sqrt{x^2 — 8x + 16 + y^2}\)
\(BD = \sqrt{(x — 0)^2 + (y — 6)^2} = \sqrt{x^2 + y^2 — 12y + 36}\)
Поскольку OD = AD = BD, составим уравнение:
\(x^2 + y^2 = x^2 — 8x + 16 + y^2\)
Упрощая, получаем:
\(0 = -8x + 16\)
Отсюда находим:
\(8x = 16 \Rightarrow x = 2\)
Теперь подставим \(x = 2\) в уравнение для \(BD\):
\(x^2 + y^2 = x^2 + y^2 — 12y + 36\)
Упрощаем:
\(0 = -12y + 36\)
Отсюда:
\(12y = 36 \Rightarrow y = 3\)
Таким образом, координаты центра описанной окружности D(2, 3, 0).
Теперь найдем радиус окружности:
\(R_{ΔABC} = |OD| = \sqrt{x^2 + y^2} = \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13}\)
Теперь перейдем ко второй части задачи — нахождению координат точки D(x, y, z), равноудалённой от вершин тетраэдра ΟABC.
Снова используем формулу для расстояния:
\(OD = AD = BD = CD\)
Где:
\(OD = \sqrt{x^2 + y^2 + z^2}\)
\(AD = \sqrt{(x — 4)^2 + (y — 0)^2 + (z — 0)^2} = \sqrt{x^2 — 8x + 16 + y^2 + z^2}\)
\(BD = \sqrt{(x — 0)^2 + (y — 6)^2 + (z — 0)^2} = \sqrt{x^2 + y^2 — 12y + 36 + z^2}\)
\(CD = \sqrt{(x — 0)^2 + (y — 0)^2 + (z + 2)^2} = \sqrt{x^2 + y^2 + 4z + 4}\)
Составим уравнения, приравнивая расстояния:
\(x^2 + y^2 + z^2 = x^2 — 8x + 16 + y^2 + z^2\)
Упрощаем:
\(0 = -8x + 16 \Rightarrow 8x = 16 \Rightarrow x = 2\)
Теперь подставим \(x = 2\) в уравнение для \(BD\):
\(x^2 + y^2 + z^2 = x^2 + y^2 — 12y + 36 + z^2\)
Упрощаем:
\(0 = -12y + 36 \Rightarrow 12y = 36 \Rightarrow y = 3\)
Теперь подставим \(x = 2\) и \(y = 3\) в уравнение для \(CD\):
\(x^2 + y^2 + z^2 = x^2 + y^2 + 4z + 4\)
Упрощаем:
\(0 = 4z + 4 \Rightarrow 4z = -4 \Rightarrow z = -1\)
Таким образом, координаты точки D, равноудалённой от вершин тетраэдра ΟABC, равны D(2, 3, -1).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!