
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 671 Атанасян — Подробные Ответы
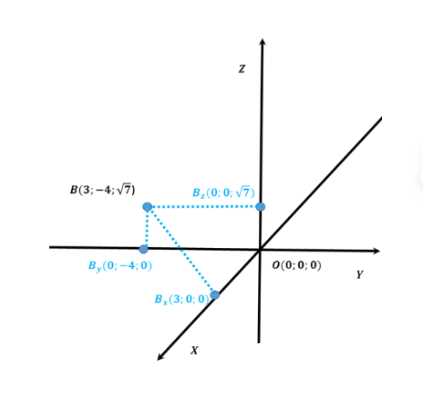
На каждой из осей координат найдите такую точку, расстояние от которой до точки В (3; -4; 7) является наименьшим среди всех расстояний от точек этой оси до точки В.
Решение:
Для оси X точка с наименьшим расстоянием до точки В — \(B_x(3; 0; 0)\).
Для оси Y точка с наименьшим расстоянием до точки В — \(B_y(0; -4; 0)\).
Для оси Z точка с наименьшим расстоянием до точки В — \(B_z(0; 0; 7)\).
Решение:
Для нахождения точек на каждой из осей координат, расстояние до которых от точки В (3; -4; 7) является минимальным, необходимо воспользоваться геометрическим подходом.
Рассмотрим каждую ось по отдельности:
Ось X:
Точка В имеет координату \(x = 3\) на оси X. Следовательно, точка с наименьшим расстоянием до В на оси X будет иметь координату \(x = 3\). Таким образом, точка \(B_x(3; 0; 0)\) является ближайшей к точке В на оси X.
Ось Y:
Точка В имеет координату \(y = -4\) на оси Y. Следовательно, точка с наименьшим расстоянием до В на оси Y будет иметь координату \(y = -4\). Таким образом, точка \(B_y(0; -4; 0)\) является ближайшей к точке В на оси Y.
Ось Z:
Точка В имеет координату \(z = 7\) на оси Z. Следовательно, точка с наименьшим расстоянием до В на оси Z будет иметь координату \(z = 7\). Таким образом, точка \(B_z(0; 0; 7)\) является ближайшей к точке В на оси Z.
Таким образом, точки \(B_x(3; 0; 0)\), \(B_y(0; -4; 0)\) и \(B_z(0; 0; 7)\) являются ближайшими к точке В (3; -4; 7) на соответствующих осях координат.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!