
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 634 Атанасян — Подробные Ответы
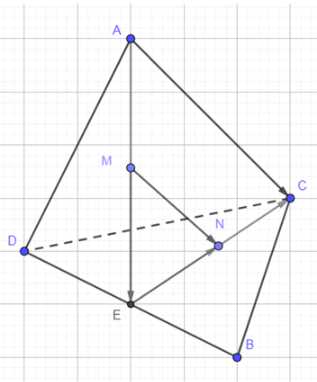
В тетраэдре \(ABCD\) точки \(М\) и \(N\) являются соответственно точками пересечения медиан граней \(ADB\) и \(BDC\). Докажите, что \(MN \parallel АС\), и найдите отношение длин этих отрезков
В тетраэдре ABCD точки M и N являются соответственно точками пересечения медиан граней ADB и BDC. Докажем, что MN || AC и найдем отношение длин этих отрезков.
1) Пусть точка E — середина ребра BD, тогда по свойству медиан треугольника M ∈ AE и N ∈ CE.
2) Используя свойство пропорциональности отрезков, получаем: AE = 3ME и EC = 3EN.
3) Следовательно, AC = AE + EC = 3ME + 3EN = 3(ME + EN) = 3MN.
4) Таким образом, векторы AC и MN коллинеарны, значит MN || AC.
5) Отношение длин отрезков MN и AC равно:
\(\frac{MN}{AC} = \frac{1}{3}\)
Ответ: MN || AC, \(\frac{MN}{AC} = \frac{1}{3}\).
В данной задаче требуется доказать, что в тетраэдре ABCD точки пересечения медиан M и N являются коллинеарными с ребром AC, а также найти отношение длин отрезков MN и AC.
Шаг 1. Рассмотрим точку E — середину ребра BD тетраэдра ABCD.
Согласно свойству медиан треугольника, точки M и N являются серединами отрезков AE и CE соответственно.
Шаг 2. Используя свойство пропорциональности отрезков, можно записать:
AE = 3ME и EC = 3EN
Шаг 3. Найдем длину ребра AC:
AC = AE + EC = 3ME + 3EN = 3(ME + EN) = 3MN
Шаг 4. Из равенства AC = 3MN следует, что векторы AC и MN коллинеарны, то есть MN || AC.
Шаг 5. Найдем отношение длин отрезков MN и AC:
\(\frac{MN}{AC} = \frac{MN}{3MN} = \frac{1}{3}\)
Таким образом, мы доказали, что в тетраэдре ABCD точки пересечения медиан M и N коллинеарны с ребром AC, а отношение длин отрезков MN и AC равно \(\frac{1}{3}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!