
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 622 Атанасян — Подробные Ответы
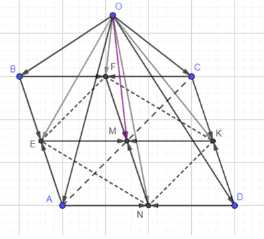
Отрезки, соединяющие середины противоположных сторон четырёхугольника \(ABCD\), пересекаются в точке \(М\). Точка \(О\) — произвольная точка пространства. Докажите, что справедливо равенство \(\vec{ОМ} = \frac{1}{4}(\vec{ОА} + \vec{ОВ} + \vec{ОС} + \vec{ОD})\).
Доказательство: 1) \(\vec{ОЕ} = \vec{ОА} + \vec{АЕ}\), тогда \(2\vec{ОЕ} = \vec{ОВ} + \vec{ВЕ} + \vec{ОА} + \vec{АЕ}\), и так как \(\vec{ВЕ} = -\vec{АЕ}\), то \(\vec{ОЕ} = \frac{1}{2}(\vec{ОА} + \vec{ОВ})\). 2) Аналогично \(\vec{ОF} = \frac{1}{2}(\vec{ОВ} + \vec{ОС})\), \(\vec{ОК} = \frac{1}{2}(\vec{ОС} + \vec{ОD})\) и \(\vec{ОN} = \frac{1}{2}(\vec{ОD} + \vec{ОА})\). 3) \(\vec{ОМ} = \vec{ОF} + \vec{FM} = \vec{ОN} + \vec{NM} = \vec{ОЕ} + \vec{ЕМ} = \vec{ОК} + \vec{КМ}\). 4) \(\vec{ЕF} = \vec{NK} = \frac{1}{2}\vec{AC}\), \(\vec{ЕN} = \vec{FK}\), значит четырехугольник \(EFKN\) является ромбом, откуда \(\vec{FM} = -\vec{NM}\) и \(\vec{ЕМ} = -\vec{КМ}\). 5) \(4\vec{ОМ} = \vec{ОF} + \vec{ОЕ} + \vec{ОК} + \vec{ОN}\), следовательно \(\vec{ОМ} = \frac{1}{4}(\vec{ОА} + \vec{ОВ} + \vec{ОС} + \vec{ОD})\).\).
Дано четырехугольник \(ABCD\), где \(E\), \(F\), \(K\), \(N\) — середины сторон \(AB\), \(BC\), \(CD\), \(DA\) соответственно, и точка \(M\) является пересечением отрезков \(EK\) и \(FN\). Произвольная точка в пространстве обозначена как \(O\). Необходимо доказать, что вектор \(\vec{ОМ}\) равен \(\frac{1}{4}(\vec{ОА} + \vec{ОВ} + \vec{ОС} + \vec{ОD})\).
Доказательство:
1) Рассмотрим вектор \(\vec{ОЕ}\). Он равен сумме векторов \(\vec{ОВ}\) и \(\vec{ВЁ}\), то есть \(\vec{ОЕ} = \vec{ОА} + \vec{АЕ}\). Удвоив обе части равенства, получим \(2\vec{ОЕ} = \vec{ОВ} + \vec{ВЕ} + \vec{ОА} + \vec{АЕ}\). Так как \(\vec{ВЕ} = -\vec{АЕ}\), то \(2\vec{ОЕ} = \vec{ОА} + \vec{ОВ}\), откуда \(\vec{ОЕ} = \frac{1}{2}(\vec{ОА} + \vec{ОВ})\).
2) Аналогично можно показать, что \(\vec{ОF} = \frac{1}{2}(\vec{ОВ} + \vec{ОС})\), \(\vec{ОК} = \frac{1}{2}(\vec{ОС} + \vec{ОD})\) и \(\vec{ОN} = \frac{1}{2}(\vec{ОD} + \vec{ОА})\).
3) Рассмотрим вектор \(\vec{ОМ}\). Он может быть представлен в виде суммы различных пар векторов: \(\vec{ОМ} = \vec{ОF} + \vec{FM} = \vec{ОN} + \vec{NM} = \vec{ОЕ} + \vec{ЕМ} = \vec{ОК} + \vec{КМ}\).
4) Используя свойство средних линий в треугольниках \(ABC\) и \(ADC\), можно показать, что \(\vec{ЕF} = \vec{NK} = \frac{1}{2}\vec{AC}\) и \(\vec{ЕN} = \vec{FK}\). Таким образом, четырехугольник \(EFKN\) является ромбом, откуда следует, что \(\vec{FM} = -\vec{NM}\) и \(\vec{ЕМ} = -\vec{КМ}\).
5) Теперь можно записать, что \(4\vec{ОМ} = \vec{ОF} + \vec{ОЕ} + \vec{ОК} + \vec{ОN}\). Подставляя выражения для этих векторов, полученные ранее, получаем \(\vec{ОМ} = \frac{1}{4}(\vec{ОА} + \vec{ОВ} + \vec{ОС} + \vec{ОD})\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!