
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 617 Атанасян — Подробные Ответы
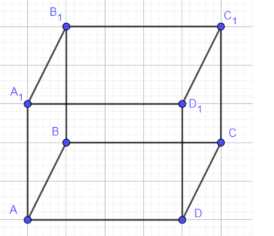
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Найдите сумму векторов: а) \(\vec{AB} + \vec{B_1C_1} + \vec{DD_1} + \vec{CD}\); б) \(\vec{B_1C_1} + \vec{AB} + \vec{DD_1} + \vec{CB_1} + \vec{BC} + \vec{A_1A}\); в) \(\vec{BА} + \vec{AС} + \vec{CВ} + \vec{DС} + \vec{DА}\).
Решение:
1) Воспользуемся сочетательным и переместительным законами, а также тем, что противоположные ребра параллелепипеда равны и параллельны:
а) \(\vec{AB} + \vec{B_1C_1} + \vec{DD_1} + \vec{CD} = (\vec{AB} + \vec{B_1C_1}) + (\vec{DD_1} + \vec{CD}) =\)
\(= (\vec{AB} + \vec{BC}) + (\vec{CD} + \vec{DD_1}) = \vec{AC} + \vec{CD_1} = \vec{AD_1}\)
б) \(\vec{B_1C_1} + \vec{AB} + \vec{DD_1} + \vec{CB_1} + \vec{BC} + \vec{A_1A} = (\vec{CB_1} +\)
\(+ \vec{B_1C_1}) + (\vec{AB} + \vec{BC}) + (\vec{DD_1} + \vec{A_1A}) = \)
\(=\vec{CC_1} + \vec{AC} + (\vec{DD_1} + \vec{D_1D}) = \vec{AC} + \vec{CC_1} + 0 = \vec{AG}\)
в) \(\vec{BА} + \vec{AС} + \vec{CВ} + \vec{DС} + \vec{DА} = (\vec{DA} + \vec{AC}) + \)
\(+(\vec{DC} + \vec{CB}) + \vec{BА} = \vec{DC} + \vec{DB} + \vec{BА} = \vec{DC} + \vec{DA} = \vec{DB}\) (по правилу параллелограмма)
Ответ:
а) \(\vec{AD_1}\)
б) \(\vec{AG}\)
в) \(\vec{DB}\)
Дано: параллелепипед \(ABCDA_1B_1C_1D_1\). Требуется найти:
а) \(\vec{AB} + \vec{B_1C_1} + \vec{DD_1} + \vec{CD}\)
б) \(\vec{B_1C_1} + \vec{AB} + \vec{DD_1} + \vec{CB_1} + \vec{BC} + \vec{A_1A}\)
в) \(\vec{BА} + \vec{AС} + \vec{CВ} + \vec{DС} + \vec{DА}\)
Решение:
а) Воспользуемся сочетательным и переместительным законами, а также тем, что противоположные ребра параллелепипеда равны и параллельны:
\(\vec{AB} + \vec{B_1C_1} + \vec{DD_1} + \vec{CD} = (\vec{AB} + \vec{B_1C_1}) + (\vec{DD_1} + \vec{CD}) =\)
\( =(\vec{AB} + \vec{BC}) + (\vec{CD} + \vec{DD_1}) = \vec{AC} + \vec{CD_1} = \vec{AD_1}\)
б) Аналогично:
\(\vec{B_1C_1} + \vec{AB} + \vec{DD_1} + \vec{CB_1} + \vec{BC} + \vec{A_1A} = (\vec{CB_1} + \)
\(+\vec{B_1C_1}) + (\vec{AB} + \vec{BC}) + (\vec{DD_1} + \vec{A_1A}) =\)
\(= \vec{CC_1} + \vec{AC} + (\vec{DD_1} + \vec{D_1D}) = \vec{AC} + \vec{CC_1} + 0 = \vec{AG}\)
в) Используя правило параллелограмма:
\(\vec{BА} + \vec{AС} + \vec{CВ} + \vec{DС} + \vec{DА} = (\vec{DA} + \vec{AC}) + (\vec{DC} +\)
\(+ \vec{CB}) + \vec{BА} = \vec{DC} + \vec{DB} + \vec{BА} = \vec{DC} + \vec{DA} = \vec{DB}\)
Ответ:
а) \(\vec{AD_1}\)
б) \(\vec{AG}\)
в) \(\vec{DB}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!