
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 608 Атанасян — Подробные Ответы
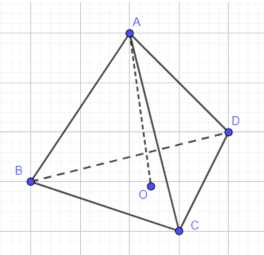
В тетраэдре \(ABCD\) медианы грани \(BCD\) пересекаются в точке \(О\). Докажите, что длина отрезка \(АО\) меньше одной трети суммы длин рёбер с общей вершиной \(А\).
Доказательство:
1) Из задачи 366 известно, что \(AO = \frac{1}{3}(AB + AC + AD)\)
2) Из задачи 350 следует, что \(AO \leq AB + AC + AD\)
3) Следовательно, \(AO \leq \frac{1}{3}(AB + AC + AD)\)
Дано: тетраэдр \(ABCD\), точка \(O\) — пересечение медиан грани \(BCD\). Требуется доказать, что \(AO \leq \frac{1}{3}(AB + AC + AD)\).
Доказательство:
1) Точка \(O\) является пересечением медиан грани \(BCD\) тетраэдра \(ABCD\). Из теоремы 366 известно, что медианы тетраэдра пересекаются в одной точке, и расстояние от этой точки до вершин тетраэдра равно одной трети соответствующих рёбер. Таким образом, \(AO = \frac{1}{3}(AB + AC + AD)\).
2) Из теоремы 350 следует, что для любой точки \(P\) внутри тетраэдра \(ABCD\) выполняется неравенство \(AP \leq AB + AC + AD\). Поскольку точка \(O\) является внутренней точкой тетраэдра, то \(AO \leq AB + AC + AD\).
3) Сравнивая выражения, полученные в пунктах 1 и 2, видим, что \(AO \leq \frac{1}{3}(AB + AC + AD)\).
Таким образом, доказано, что \(AO \leq \frac{1}{3}(AB + AC + AD)\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!