
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 603 Атанасян — Подробные Ответы
Докажите, что если \(М\) — точка пересечения медиан треугольника \(АВС\), а \(О\) — произвольная точка пространства, то \(\vec{ОМ} = \frac{1}{3}(\vec{ОА} + \vec{ОВ} + \vec{ОС})\).
Решение
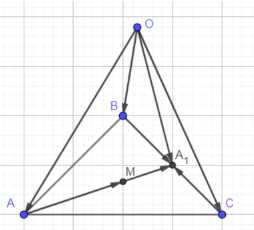
По теореме о точке пересечения медиан треугольника \(АМ = 2МА_1\), где \(АА_1\) — медиана треугольника \(АВС\) (рис. 170). Согласно задаче 586 \(\vec{ОМ} = \frac{\vec{ОА} + 2\vec{ОА_1}}{1 + 2} = \frac{\vec{ОА} + 2\vec{ОА_1}}{3}\). Но \(\vec{ОА_1} = \frac{1}{2}(\vec{ОВ} + \vec{ОС})\) (объясните почему), поэтому \(\vec{ОМ} = \frac{\vec{ОА} + \vec{ОВ} + \vec{ОС}}{3}\).
Доказательство:
\(\vec{ОМ} = \frac{1}{3}(\vec{ОА} + \vec{ОВ} + \vec{ОС})\)
Доказательство:
По теореме о точке пересечения медиан треугольника \(АМ = 2МА_1\), где \(АА_1\) — медиана треугольника \(АВС\). Согласно задаче 586 \(\vec{ОМ} = \frac{\vec{ОА} + 2\vec{ОА_1}}{1 + 2} = \frac{\vec{ОА} + 2\vec{ОА_1}}{3}\). Но \(\vec{ОА_1} = \frac{1}{2}(\vec{ОВ} + \vec{ОС})\), так как \(ОА_1\) является медианой треугольника \(АВС\). Поэтому \(\vec{ОМ} = \frac{\vec{ОА} + 2\cdot\frac{1}{2}(\vec{ОВ} + \vec{ОС})}{3} = \frac{\vec{ОА} + \vec{ОВ} + \vec{ОС}}{3}\).
Доказательство:
Пусть \(М\) — точка пересечения медиан треугольника \(АВС\), а \(О\) — произвольная точка пространства. Необходимо доказать, что \(\vec{ОМ} = \frac{1}{3}(\vec{ОА} + \vec{ОВ} + \vec{ОС})\).
Доказательство:
1. По теореме о точке пересечения медиан треугольника, \(АМ = 2МА_1\), где \(АА_1\) — медиана треугольника \(АВС\).
2. Согласно задаче 586, \(\vec{ОМ} = \frac{\vec{ОА} + 2\vec{ОА_1}}{1 + 2} = \frac{\vec{ОА} + 2\vec{ОА_1}}{3}\).
3. Поскольку \(ОА_1\) является медианой треугольника \(АВС\), то \(\vec{ОА_1} = \frac{1}{2}(\vec{ОВ} + \vec{ОС})\).
4. Подставляя выражение для \(\vec{ОА_1}\) в формулу для \(\vec{ОМ}\), получаем:
\(\vec{ОМ} = \frac{\vec{ОА} + 2\cdot\frac{1}{2}(\vec{ОВ} + \vec{ОС})}{3} = \frac{\vec{ОА} + \vec{ОВ} + \vec{ОС}}{3}\).
Таким образом, мы доказали, что \(\vec{ОМ} = \frac{1}{3}(\vec{ОА} + \vec{ОВ} + \vec{ОС})\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!