ГДЗ по Геометрии 11 класс Номер 597 Атанасян — Подробные Ответы

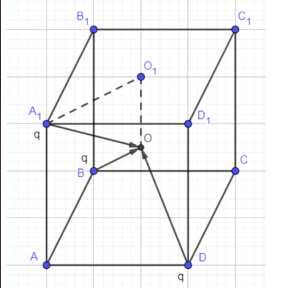
В вершинах \(A_1\), \(B\) и \(D\) куба \(ABCDA_1B_1C_1D_1\), ребро которого равно \(a\), помещены точечные заряды \(q\). а) Выразите результирующую напряжённость создаваемого ими электрического поля в точках \(А\) и \(С_1\) через вектор \(\vec{АС_1}\). б) Найдите абсолютную величину результирующей напряжённости в точках \(С\), \(В_1\), в центре грани \(A_1B_1C_1D_1\) и в центре куба.

В вершинах \(A_1\), \(B\) и \(D\) куба \(ABCDA_1B_1C_1D_1\), ребро которого равно \(a\), помещены точечные заряды \(q\). Результирующая напряженность поля в точке \(А\) равна \(\vec{E} = \frac{kq}{a^3} (\vec{A_1A} + \vec{BA} + \vec{DA})\). Используя правило параллелепипеда, \(\vec{A_1A} + \vec{BA} + \vec{DA} = -\vec{AA_1} — \vec{AB} — \vec{AD} = -\vec{AC_1}\), тогда \(\vec{E} = -\frac{kq}{a^3} \vec{AC_1}\). Результирующая напряженность поля в точке \(C_1\) равна \(\vec{E} = \frac{kq}{A_1C_1^3} \vec{A_1C_1} + \frac{kq}{BC_1^3} \vec{BC_1} + \frac{kq}{DC_1^3} \vec{DC_1}\). Поскольку \(A_1C_1 = BC_1 = DC_1 = a\sqrt{2}\), то \(\vec{E} = \frac{kq}{(a\sqrt{2})^3} (\vec{A_1C_1} + \vec{BC_1} + \vec{DC_1})\). Сумма векторов \(\vec{A_1C_1} + \vec{BC_1} + \vec{DC_1} = 2\vec{AC_1}\). Тогда \(\vec{E} = \frac{kq}{2\sqrt{2}a^3} (2\vec{AC_1}) = \frac{\sqrt{2}kq}{2a^3} \vec{AC_1}\).

Абсолютная величина результирующего поля в точке \(С\) определяется суммой векторов напряженности от зарядов в \(A_1\), \(B\), \(D\). Расстояния до зарядов равны \(A_1C = a\sqrt{3}\), \(BC = a\), \(DC = a\). Модуль напряженности в точке \(С\) равен \(|\vec{E}| = \frac{kq}{3a^2} \sqrt{19 + 4\sqrt{3}}\). В точке \(В_1\) из соображений симметрии модуль напряженности равен \(|\vec{E}| = \frac{kq}{3a^2} \sqrt{19 + 4\sqrt{3}}\). В центре грани \(A_1B_1C_1D_1\) (точка \(O_1\)) расстояния до зарядов равны \(A_1O_1 = \frac{a}{\sqrt{2}}\), \(BO_1 = a\sqrt{\frac{3}{2}}\), \(DO_1 = a\sqrt{\frac{3}{2}}\). Модуль напряженности в точке \(O_1\) равен \(|\vec{E}| = \frac{2kq}{9a^2} \sqrt{105}\). В центре куба (точка \(O\)) расстояния до зарядов равны \(A_1O = BO = DO = \frac{a\sqrt{3}}{2}\). Модуль напряженности в точке \(O\) равен \(|\vec{E}| = \frac{4kq}{3a^2}\).

Дано: \(ABCDA_1B_1C_1D_1\) — куб; \(a\) — ребро куба; в вершинах \(A_1\), \(B\) и \(D\) находятся точечные заряды \(q\).
Найти: а) Результирующую напряженность поля в точках \(A\) и \(C_1\) через вектор \(\vec{AC_1}\); б) Абсолютную величину результирующего поля в точках \(C\), \(B_1\), в центре грани \(A_1B_1C_1D_1\) и в центре куба.
Решение:
а) Результирующая напряженность поля в точке \(A\):
Напряженность поля в точке \(A\) создается зарядами в точках \(A_1\), \(B\) и \(D\). Вектор напряженности от точечного заряда определяется как \(\vec{E} = k \frac{q}{r^3} \vec{r}\), где \(\vec{r}\) — радиус-вектор, направленный от заряда к точке наблюдения.
\(\vec{E}_A = \frac{kq}{A_1A^3}\vec{A_1A} + \frac{kq}{BA^3}\vec{BA} + \frac{kq}{DA^3}\vec{DA}\).
Расстояния от зарядов до точки \(A\) равны длине ребра куба: \(A_1A = BA = DA = a\).
Следовательно, \(\vec{E}_A = \frac{kq}{a^3}\vec{A_1A} + \frac{kq}{a^3}\vec{BA} + \frac{kq}{a^3}\vec{DA} = \frac{kq}{a^3}(\vec{A_1A} + \vec{BA} + \vec{DA})\).
Векторы \(\vec{A_1A}\), \(\vec{BA}\), \(\vec{DA}\) направлены от вершин \(A_1\), \(B\), \(D\) к вершине \(A\). Их можно выразить через векторы ребер, выходящих из \(A\): \(\vec{A_1A} = -\vec{AA_1}\), \(\vec{BA} = -\vec{AB}\), \(\vec{DA} = -\vec{AD}\).
Тогда \(\vec{A_1A} + \vec{BA} + \vec{DA} = -\vec{AA_1} — \vec{AB} — \vec{AD}\).
Векторы \(\vec{AA_1}\), \(\vec{AB}\), \(\vec{AD}\) являются взаимно перпендикулярными ребрами куба, выходящими из вершины \(A\). Их сумма по правилу параллелепипеда равна вектору пространственной диагонали \(\vec{AC_1}\): \(\vec{AA_1} + \vec{AB} + \vec{AD} = \vec{AC_1}\).
Следовательно, \(-\vec{AA_1} — \vec{AB} — \vec{AD} = -(\vec{AA_1} + \vec{AB} + \vec{AD}) = -\vec{AC_1}\).
Тогда \(\vec{E}_A = \frac{kq}{a^3}(-\vec{AC_1}) = -\frac{kq}{a^3}\vec{AC_1}\).

Результирующая напряженность поля в точке \(C_1\):
Напряженность поля в точке \(C_1\) создается зарядами в точках \(A_1\), \(B\) и \(D\).
\(\vec{E}_{C_1} = \frac{kq}{A_1C_1^3}\vec{A_1C_1} + \frac{kq}{BC_1^3}\vec{BC_1} + \frac{kq}{DC_1^3}\vec{DC_1}\).
Расстояния от зарядов до точки \(C_1\) — это длины диагоналей граней куба: \(A_1C_1\), \(BC_1\), \(DC_1\). Длина диагонали грани куба с ребром \(a\) равна \(a\sqrt{2}\).
\(A_1C_1 = BC_1 = DC_1 = a\sqrt{2}\).
Куб расстояния: \((a\sqrt{2})^3 = a^3 (\sqrt{2})^3 = a^3 \cdot 2\sqrt{2}\).
Следовательно, \(A_1C_1^3 = BC_1^3 = DC_1^3 = 2\sqrt{2}a^3\).
Тогда \(\vec{E}_{C_1} = \frac{kq}{2\sqrt{2}a^3}\vec{A_1C_1} + \frac{kq}{2\sqrt{2}a^3}\vec{BC_1} + \frac{kq}{2\sqrt{2}a^3}\vec{DC_1} = \frac{kq}{2\sqrt{2}a^3}(\vec{A_1C_1} + \vec{BC_1} + \vec{DC_1})\).
Выразим векторы \(\vec{A_1C_1}\), \(\vec{BC_1}\), \(\vec{DC_1}\) через векторы ребер.
\(\vec{A_1C_1} = \vec{A_1D_1} + \vec{D_1C_1}\) (векторное сложение в грани \(A_1B_1C_1D_1\)).
\(\vec{BC_1} = \vec{BC} + \vec{CC_1}\) (векторное сложение в грани \(BCC_1B_1\)).
\(\vec{DC_1} = \vec{DD_1} + \vec{D_1C_1}\) (векторное сложение в грани \(DCC_1D_1\)).
Сумма векторов: \(\vec{A_1C_1} + \vec{BC_1} + \vec{DC_1} = (\vec{A_1D_1} + \vec{D_1C_1}) + (\vec{BC} + \vec{CC_1}) + (\vec{DD_1} + \vec{D_1C_1})\).
Сгруппируем и заменим векторы параллельными ребрами, выходящими из \(A\): \(\vec{A_1D_1} = \vec{AD}\), \(\vec{D_1C_1} = \vec{AB}\), \(\vec{BC} = \vec{AD}\), \(\vec{CC_1} = \vec{AA_1}\), \(\vec{DD_1} = \vec{AA_1}\).
Сумма = \(\vec{AD} + \vec{AB} + \vec{AD} + \vec{AA_1} + \vec{AA_1} + \vec{AB} = 2\vec{AD} + 2\vec{AB} + 2\vec{AA_1} = \)
\(=2(\vec{AD} + \vec{AB} + \vec{AA_1})\).
По правилу параллелепипеда \(\vec{AD} + \vec{AA_1} + \vec{AB} = \vec{AC_1}\).
Таким образом, \(\vec{A_1C_1} + \vec{BC_1} + \vec{DC_1} = 2\vec{AC_1}\).
Подставляем это в выражение для \(\vec{E}_{C_1}\):
\(\vec{E}_{C_1} = \frac{kq}{2\sqrt{2}a^3} \cdot 2\vec{AC_1} = \frac{2kq}{2\sqrt{2}a^3}\vec{AC_1} = \frac{kq}{\sqrt{2}a^3}\vec{AC_1}\).
Умножим числитель и знаменатель на \(\sqrt{2}\) для избавления от иррациональности в знаменателе:
\(\vec{E}_{C_1} = \frac{kq\sqrt{2}}{\sqrt{2}\sqrt{2}a^3}\vec{AC_1} = \frac{\sqrt{2}kq}{2a^3}\vec{AC_1}\).
б) Результирующая напряженность поля в точке С:
\( \vec{E} = \frac{kq}{A_1C} \cdot \frac{\vec{A_1C}}{A_1C} + \frac{kq}{a^3} \cdot \vec{BC} + \frac{kq}{a^3} \cdot \vec{DC} \)
\( A_1C = \sqrt{A_1A^2 + AC^2} = \sqrt{a^2 + a^2 \cdot 2} = \sqrt{3a^2} = a\sqrt{3} \), тогда
\( \vec{E} = \frac{kq}{a^3} \left( \frac{\sqrt{3}}{9} \vec{A_1C} + \left(1 + \frac{\sqrt{3}}{9}\right) \vec{BC} + \left(1 + \frac{\sqrt{3}}{9}\right) \vec{DC} \right) \);
\( \vec{E} \) – диагональ параллелепипеда со сторонами \( \frac{kq\sqrt{3}}{a^3} \cdot \frac{\sqrt{3}}{9} \vec{A_1C} \), \( \frac{kq}{a^3} \left(1 + \frac{\sqrt{3}}{9}\right) \vec{BC} \) и \( \frac{kq}{a^3} \left(1 + \frac{\sqrt{3}}{9}\right) \vec{DC} \) (по правилу параллелепипеда);
значит его модуль равен:
\( |\vec{E}| = \frac{kq}{a^3} \sqrt{\left(\frac{\sqrt{3}}{9}a\right)^2 + \left(\left(1 + \frac{\sqrt{3}}{9}\right)a\right)^2 + \left(\left(1 + \frac{\sqrt{3}}{9}\right)a\right)^2} = \frac{kq}{3a^2} \sqrt{19 + 4\sqrt{3}} \);
Результирующая напряженность поля в точке В:
\( \vec{E} = \frac{kq}{DB_1} \cdot \frac{\vec{DB_1}}{DB_1} + \frac{kq}{a^3} \cdot \vec{BB_1} + \frac{kq}{a^3} \cdot \vec{A_1B_1} \);
\( DB_1 = A_1C \), тогда \( \vec{E} = \frac{kq}{a^3} \left( \frac{\sqrt{3}}{9} \vec{DB_1} + \left(1 + \frac{\sqrt{3}}{9}\right) \vec{BB_1} + \left(1 + \frac{\sqrt{3}}{9}\right) \vec{A_1B_1} \right) \);
Значит, как и в предыдущем примере \( |\vec{E}| = \frac{kq}{3a^2} \sqrt{19 + 4\sqrt{3}} \);
Результирующая напряженность поля в точке О:
\( \vec{E} = \frac{kq}{A_1O} \cdot \frac{\vec{A_1O}}{A_1O} + \frac{kq}{DO} \cdot \frac{\vec{DO}}{DO} + \frac{kq}{BO} \cdot \frac{\vec{BO}}{BO} \);
\( BO = DO = A_1O = \sqrt{\left(\frac{1}{2} a\sqrt{2}\right)^2 + \left(\frac{1}{2} a\right)^2} = a \sqrt{\frac{3}{4}} \), тогда
\( \vec{E} = \frac{4\sqrt{4}kq}{3\sqrt{3}a^3} (\vec{BO} + \vec{DO} + \vec{A_1O}) \);
\( \vec{BO} + \vec{DO} = 2\vec{OO_1} = \vec{AA_1} \) (по правилу параллелограмма);
\( \vec{AA_1} + \vec{A_1O} = \vec{AO} \), тогда \( |\vec{AO}| = A_1O = a \sqrt{\frac{3}{4}} \);
Таким образом: \( \vec{E} = \frac{4\sqrt{4}kq}{3\sqrt{3}a^3} \cdot a \sqrt{\frac{3}{4}} = \frac{4kq}{3a^2} \);
Ответ: а) \( -\frac{kq}{a^3} \vec{AC_1} \); \( \frac{\sqrt{2}kq}{2a^3} \vec{AC_1} \); б) \( \frac{kq}{3a^2} \sqrt{19 + 4\sqrt{3}} \); \( \frac{kq}{3a^2} \sqrt{19 + 4\sqrt{3}} \); \( \frac{2kq}{9a^2} \sqrt{105} \); \( \frac{4kq}{3a^2} \);