
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 595 Атанасян — Подробные Ответы
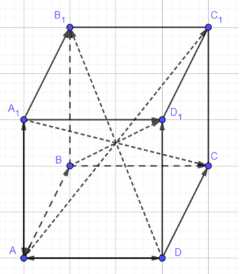
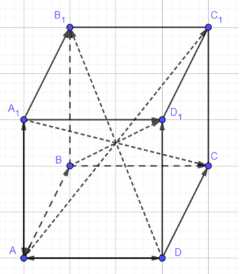
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: а) \(\vec{AB} + \vec{AD} + \vec{AA_1}\); б) \(\vec{DA} + \vec{DC} + \vec{DD_1}\); в) \(\vec{A_1B_1} + \vec{C_1B_1} + \vec{BB_1}\); г) \(\vec{А_1А} + \vec{AD_1} + \vec{АВ}\); д) \(\vec{В_1А_1} + \vec{ВВ_1} + \vec{ВС}\).
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Найти вектор, равный сумме векторов:
а) \(\vec{AB} + \vec{AD} + \vec{AA_1}\). Ответ: \(\vec{AC_1}\).
б) \(\vec{DA} + \vec{DC} + \vec{DD_1}\). Ответ: \(\vec{DB_1}\).
в) \(\vec{A_1B_1} + \vec{C_1B_1} + \vec{BB_1}\). Ответ: \(\vec{DB_1}\).
г) \(\vec{А_1А} + \vec{AD_1} + \vec{АВ}\). Ответ: \(\vec{A_1C}\).
д) \(\vec{В_1А_1} + \vec{ВВ_1} + \vec{ВС}\). Ответ: \(\vec{BD_1}\).
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Требуется найти вектор, равный сумме заданных векторов.
а) Сумма векторов \(\vec{AB} + \vec{AD} + \vec{AA_1}\).
В параллелепипеде \(ABCDA_1B_1C_1D_1\), векторы \(\vec{AB}\) и \(\vec{AD}\) лежат в плоскости основания \(ABCD\). По правилу параллелограмма для векторов, исходящих из одной точки, сумма векторов \(\vec{AB}\) и \(\vec{AD}\) равна вектору диагонали параллелограмма \(ABCD\), исходящей из той же точки, то есть \(\vec{AB} + \vec{AD} = \vec{AC}\).
Теперь рассмотрим сумму \(\vec{AC} + \vec{AA_1}\). Вектор \(\vec{AC}\) лежит в плоскости основания \(ABCD\), а вектор \(\vec{AA_1}\) направлен по ребру, перпендикулярному основанию (или параллельному ему). Векторы \(\vec{AC}\) и \(\vec{AA_1}\) являются смежными сторонами параллелепипеда, построенного на этих векторах. Сумма трех векторов, исходящих из одной вершины параллелепипеда и направленных вдоль его смежных ребер, равна вектору диагонали параллелепипеда, исходящей из той же вершины. В данном случае, векторы \(\vec{AB}\), \(\vec{AD}\) и \(\vec{AA_1}\) являются такими векторами (или им равными). Их сумма равна вектору \(\vec{AC_1}\), который является диагональю параллелепипеда, исходящей из вершины \(A\).
Таким образом, \(\vec{AB} + \vec{AD} + \vec{AA_1} = (\vec{AB} + \vec{AD}) + \vec{AA_1} = \vec{AC} + \vec{AA_1} = \vec{AC_1}\).
Ответ: \(\vec{AC_1}\).
б) Сумма векторов \(\vec{DA} + \vec{DC} + \vec{DD_1}\).
Векторы \(\vec{DA}\) и \(\vec{DC}\) лежат в плоскости основания \(ABCD\) и исходят из вершины \(D\). По правилу параллелограмма, их сумма равна вектору диагонали параллелограмма \(ABCD\), исходящей из вершины \(D\), то есть \(\vec{DA} + \vec{DC} = \vec{DB}\).
Теперь рассмотрим сумму \(\vec{DB} + \vec{DD_1}\). Вектор \(\vec{DB}\) является диагональю основания, а вектор \(\vec{DD_1}\) направлен вдоль ребра, перпендикулярного основанию. Векторы \(\vec{DB}\) и \(\vec{DD_1}\) являются смежными сторонами параллелограмма \(DBB_1D_1\). По правилу параллелограмма, их сумма равна вектору диагонали этого параллелограмма, исходящей из вершины \(D\), то есть \(\vec{DB} + \vec{DD_1} = \vec{DB_1}\).
Таким образом, \(\vec{DA} + \vec{DC} + \vec{DD_1} = (\vec{DA} + \vec{DC}) + \vec{DD_1} = \vec{DB} + \vec{DD_1} = \vec{DB_1}\).
Ответ: \(\vec{DB_1}\).
в) Сумма векторов \(\vec{A_1B_1} + \vec{C_1B_1} + \vec{BB_1}\).
В параллелепипеде \(ABCDA_1B_1C_1D_1\), противоположные ребра равны и параллельны, следовательно, равны и соответствующие им векторы.
Вектор \(\vec{A_1B_1}\) равен вектору \(\vec{AB}\) и вектору \(\vec{DC}\). Возьмем \(\vec{A_1B_1} = \vec{DC}\).
Вектор \(\vec{C_1B_1}\) равен вектору \(\vec{CB}\) и вектору \(\vec{DA}\). Возьмем \(\vec{C_1B_1} = \vec{DA}\).
Вектор \(\vec{BB_1}\) равен вектору \(\vec{AA_1}\) и вектору \(\vec{DD_1}\). Возьмем \(\vec{BB_1} = \vec{DD_1}\).
Подставим эти равенства в исходную сумму: \(\vec{A_1B_1} + \vec{C_1B_1} + \vec{BB_1} = \vec{DC} + \vec{DA} + \vec{DD_1}\).
Полученная сумма \(\vec{DC} + \vec{DA} + \vec{DD_1}\) совпадает с суммой векторов в пункте б), только слагаемые переставлены. По свойству коммутативности сложения векторов, порядок слагаемых не влияет на сумму.
Таким образом, \(\vec{DC} + \vec{DA} + \vec{DD_1} = \vec{DA} + \vec{DC} + \vec{DD_1} = \vec{DB_1}\).
Ответ: \(\vec{DB_1}\).
г) Сумма векторов \(\vec{А_1А} + \vec{A_1D_1} + \vec{АВ}\).
Переставим слагаемые для удобства: \(\vec{А_1А} + \vec{АВ} + \vec{A_1D_1}\).
В параллелепипеде \(ABCDA_1B_1C_1D_1\), вектор \(\vec{A_1D_1}\) равен вектору \(\vec{AD}\).
Подставим это в сумму: \(\vec{А_1А} + \vec{АВ} + \vec{AD}\).
Перегруппируем слагаемые: \(\vec{А_1А} + (\vec{АВ} + \vec{AD})\).
В основании \(ABCD\), по правилу параллелограмма, \(\vec{АВ} + \vec{AD} = \vec{AC}\).
Таким образом, сумма равна \(\vec{А_1А} + \vec{AC}\).
Вектор \(\vec{А_1А}\) идет из точки \(A_1\) в точку \(A\). Вектор \(\vec{AC}\) идет из точки \(A\) в точку \(C\). По правилу треугольника сложения векторов, сумма \(\vec{А_1А} + \vec{AC}\) равна вектору, идущему из начальной точки первого вектора в конечную точку второго вектора, то есть \(\vec{A_1C}\).
Таким образом, \(\vec{А_1А} + \vec{A_1D_1} + \vec{АВ} = \vec{А_1А} + \vec{AD} + \vec{АВ} = \vec{А_1А} + (\vec{AD} + \vec{АВ}) = \vec{А_1А} + \vec{AC} = \)
\(=\vec{A_1C}\).
Ответ: \(\vec{A_1C}\).
д) Сумма векторов \(\vec{В_1А_1} + \vec{ВВ_1} + \vec{ВС}\).
Переставим слагаемые для удобства: \(\vec{ВВ_1} + \vec{В_1А_1} + \vec{ВС}\).
В параллелепипеде \(ABCDA_1B_1C_1D_1\), вектор \(\vec{В_1А_1}\) равен вектору \(\vec{ВА}\).
Подставим это в сумму: \(\vec{ВВ_1} + \vec{ВА} + \vec{ВС}\).
Перегруппируем слагаемые: \(\vec{ВВ_1} + (\vec{ВА} + \vec{ВС})\).
В основании \(ABCD\), векторы \(\vec{ВА}\) и \(\vec{ВС}\) исходят из вершины \(В\). По правилу параллелограмма, их сумма равна вектору диагонали параллелограмма \(ABCD\), исходящей из вершины \(В\), то есть \(\vec{ВА} + \vec{ВС} = \vec{BD}\).
Таким образом, сумма равна \(\vec{ВВ_1} + \vec{BD}\).
Вектор \(\vec{ВВ_1}\) идет из точки \(В\) в точку \(В_1\). Вектор \(\vec{BD}\) идет из точки \(В\) в точку \(D\). Векторы \(\vec{ВВ_1}\) и \(\vec{BD}\) являются смежными сторонами параллелограмма \(BB_1D_1D\). По правилу параллелограмма, их сумма равна вектору диагонали этого параллелограмма, исходящей из вершины \(В\), то есть \(\vec{ВВ_1} + \vec{BD} = \vec{BD_1}\).
Таким образом, \(\vec{В_1А_1} + \vec{ВВ_1} + \vec{ВС} = \vec{ВА} + \vec{ВВ_1} + \vec{ВС} = \vec{ВВ_1} + (\vec{ВА} + \vec{ВС}) = \vec{ВВ_1} + \vec{BD} =\)
\(= \vec{BD_1}\).
Ответ: \(\vec{BD_1}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!