
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 594 Атанасян — Подробные Ответы
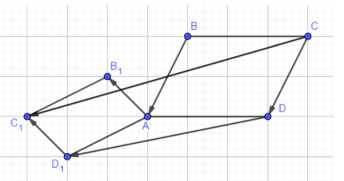
Даны параллелограммы \(ABCD\) и \(AB_1C_1D_1\). Докажите, что векторы \(\vec{BB_1}\), \(\vec{CC_1}\) и \(\vec{DD_1}\) компланарны
Из условия следует, что \(\vec{CC_1} = \vec{CD} + \vec{DD_1} + \vec{D_1C_1}\). Так как \(ABCD\) и \(AB_1C_1D_1\) параллелограммы, то \(\vec{CD} = \vec{BA}\) и \(\vec{D_1C_1} = \vec{AB_1}\). Подставляя это в первое равенство, получаем \(\vec{CC_1} = \vec{BA} + \vec{DD_1} + \vec{AB_1}\). Перегруппируем слагаемые: \(\vec{CC_1} = \vec{DD_1} + (\vec{BA} + \vec{AB_1})\). Поскольку \(\vec{BA} + \vec{AB_1} = \vec{BB_1}\), окончательно имеем \(\vec{CC_1} = \vec{DD_1} + \vec{BB_1}\). Это означает, что вектор \(\vec{CC_1}\) является линейной комбинацией векторов \(\vec{BB_1}\) и \(\vec{DD_1}\), следовательно, векторы \(\vec{BB_1}\), \(\vec{CC_1}\) и \(\vec{DD_1}\) компланарны по признаку компланарности трех векторов, что и требовалось доказать.
Дано, что \(ABCD\) и \(AB_1C_1D_1\) являются параллелограммами. Требуется доказать, что векторы \(\vec{BB_1}\), \(\vec{CC_1}\) и \(\vec{DD_1}\) компланарны.
Доказательство начинается с выражения вектора \(\vec{CC_1}\) через другие векторы. Используя правило сложения векторов по ломаной, можно записать, что \(\vec{CC_1} = \vec{CD} + \vec{DD_1} + \vec{D_1C_1}\). Это разложение вектора \(\vec{CC_1}\) на три составляющие вектора вдоль пути от точки \(C\) к точке \(C_1\) через точки \(D\) и \(D_1\).
Далее, используем свойства параллелограммов. В параллелограмме \(ABCD\) противоположные стороны параллельны и равны по длине, что означает равенство соответствующих векторов. Следовательно, вектор \(\vec{CD}\) равен вектору \(\vec{BA}\). Аналогично, в параллелограмме \(AB_1C_1D_1\) противоположные стороны также параллельны и равны, поэтому вектор \(\vec{D_1C_1}\) равен вектору \(\vec{AB_1}\).
Теперь подставим полученные векторные равенства из второго шага в выражение для вектора \(\vec{CC_1}\) из первого шага. Получаем: \(\vec{CC_1} = \vec{BA} + \vec{DD_1} + \vec{AB_1}\).
Перегруппируем слагаемые в этом выражении: \(\vec{CC_1} = \vec{DD_1} + (\vec{BA} + \vec{AB_1})\). Рассмотрим выражение в скобках \(\vec{BA} + \vec{AB_1}\). По правилу сложения векторов (правило треугольника), сумма векторов \(\vec{BA}\) и \(\vec{AB_1}\) равна вектору \(\vec{BB_1}\), то есть \(\vec{BA} + \vec{AB_1} = \vec{BB_1}\).
Подставляя это обратно в выражение для \(\vec{CC_1}\), получаем \(\vec{CC_1} = \vec{DD_1} + \vec{BB_1}\).
Это равенство показывает, что вектор \(\vec{CC_1}\) может быть представлен как линейная комбинация векторов \(\vec{DD_1}\) и \(\vec{BB_1}\) с коэффициентами, равными единице. По признаку компланарности трех векторов, если один из трех векторов может быть выражен через два других как их линейная комбинация, то эти три вектора компланарны. В данном случае, вектор \(\vec{CC_1}\) выражен через векторы \(\vec{BB_1}\) и \(\vec{DD_1}\), следовательно, векторы \(\vec{BB_1}\), \(\vec{CC_1}\) и \(\vec{DD_1}\) компланарны. Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!