Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 593 Атанасян — Подробные Ответы
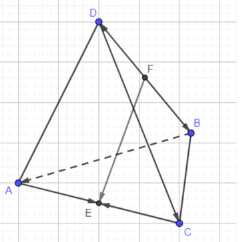
Точки \(E\) и \(F\) — середины рёбер \(AC\) и \(BD\) тетраэдра \(ABCD\). Докажите, что \(2\vec{FE} = \vec{BA} + \vec{DC}\). Компланарны ли векторы \(\vec{FE}\), \(\vec{BA}\) и \(\vec{DC}\)?
Известно, что \(E\) и \(F\) середины \(AC\) и \(BD\) соответственно. Выразим вектор \(\vec{FE}\) двумя способами: \(\vec{FE} = \vec{FD} + \vec{DC} + \vec{CE}\) и \(\vec{FE} = \vec{FB} + \vec{BA} + \vec{AE}\). Сложив эти равенства, получим \(2\vec{FE} = \vec{FD} + \vec{DC} + \vec{CE} + \vec{FB} + \vec{BA} + \vec{AE}\). Поскольку \(F\) середина \(BD\), \(\vec{FD} = -\vec{FB}\). Поскольку \(E\) середина \(AC\), \(\vec{CE} = -\vec{AE}\). Подставляя это в предыдущее равенство, имеем \(2\vec{FE} = -\vec{FB} + \vec{DC} — \vec{AE} + \vec{FB} + \vec{BA} + \vec{AE}\). Сокращая противоположные векторы, получаем \(2\vec{FE} = \vec{BA} + \vec{DC}\). Из этого равенства следует, что \(\vec{FE} = \frac{1}{2}\vec{BA} + \frac{1}{2}\vec{DC}\). Так как вектор \(\vec{FE}\) линейно выражается через векторы \(\vec{BA}\) и \(\vec{DC}\), эти три вектора являются компланарными. Ответ: да.
Рассмотрим тетраэдр \(ABCD\). Нам дано, что точка \(E\) является серединой ребра \(AC\), а точка \(F\) является серединой ребра \(BD\). Требуется доказать, что \(2\vec{FE} = \vec{BA} + \vec{DC}\), и определить, являются ли векторы \(\vec{FE}\), \(\vec{BA}\) и \(\vec{DC}\) компланарными.
Для начала выразим вектор \(\vec{FE}\) через другие векторы, используя правило сложения векторов (правило треугольника или многоугольника). Рассмотрим путь от точки \(F\) к точке \(E\) через точки \(D\) и \(C\). Вектор \(\vec{FE}\) можно представить как сумму векторов \(\vec{FD}\), \(\vec{DC}\) и \(\vec{CE}\). Таким образом, получаем первое выражение для \(\vec{FE}\): \(\vec{FE} = \vec{FD} + \vec{DC} + \vec{CE}\).
Теперь рассмотрим другой путь от точки \(F\) к точке \(E\), проходящий через точки \(B\) и \(A\). Вектор \(\vec{FE}\) также можно представить как сумму векторов \(\vec{FB}\), \(\vec{BA}\) и \(\vec{AE}\). Получаем второе выражение для \(\vec{FE}\): \(\vec{FE} = \vec{FB} + \vec{BA} + \vec{AE}\).
Сложим оба полученных выражения для вектора \(\vec{FE}\):
\(\vec{FE} + \vec{FE} = (\vec{FD} + \vec{DC} + \vec{CE}) + (\vec{FB} + \vec{BA} + \vec{AE})\)
\(2\vec{FE} = \vec{FD} + \vec{DC} + \vec{CE} + \vec{FB} + \vec{BA} + \vec{AE}\).
Теперь воспользуемся тем, что точки \(E\) и \(F\) являются серединами соответствующих отрезков. Поскольку \(E\) – середина \(AC\), векторы \(\vec{AE}\) и \(\vec{CE}\) равны по модулю и противоположно направлены, то есть \(\vec{CE} = -\vec{AE}\). Аналогично, поскольку \(F\) – середина \(BD\), векторы \(\vec{FB}\) и \(\vec{FD}\) равны по модулю и противоположно направлены, то есть \(\vec{FD} = -\vec{FB}\).
Подставим эти соотношения в выражение для \(2\vec{FE}\):
\(2\vec{FE} = (-\vec{FB}) + \vec{DC} + (-\vec{AE}) + \vec{FB} + \vec{BA} + \vec{AE}\).
Теперь сгруппируем и сократим противоположные векторы:
\(2\vec{FE} = (-\vec{FB} + \vec{FB}) + (\vec{DC}) + (-\vec{AE} + \vec{AE}) + (\vec{BA})\)
\(2\vec{FE} = \vec{0} + \vec{DC} + \vec{0} + \vec{BA}\)
\(2\vec{FE} = \vec{DC} + \vec{BA}\), или \(2\vec{FE} = \vec{BA} + \vec{DC}\).
Это завершает доказательство первого пункта задачи.
Теперь перейдем ко второму пункту: определить, являются ли векторы \(\vec{FE}\), \(\vec{BA}\) и \(\vec{DC}\) компланарными. Из доказанного равенства \(2\vec{FE} = \vec{BA} + \vec{DC}\) мы можем выразить вектор \(\vec{FE}\):
\(\vec{FE} = \frac{1}{2}\vec{BA} + \frac{1}{2}\vec{DC}\).
Векторы являются компланарными, если один из них может быть представлен как линейная комбинация двух других, то есть если существуют скаляры \(x\) и \(y\) такие, что \(\vec{a} = x\vec{b} + y\vec{c}\). В нашем случае мы видим, что вектор \(\vec{FE}\) представлен как линейная комбинация векторов \(\vec{BA}\) и \(\vec{DC}\) с коэффициентами \(x = \frac{1}{2}\) и \(y = \frac{1}{2}\). Поскольку такие скаляры существуют, векторы \(\vec{FE}\), \(\vec{BA}\) и \(\vec{DC}\) лежат в одной плоскости, то есть являются компланарными.
Таким образом, ответ на вопрос о компланарности векторов \(\vec{FE}\), \(\vec{BA}\) и \(\vec{DC}\) – да.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.