Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 592 Атанасян — Подробные Ответы
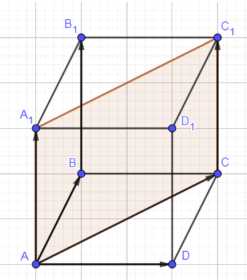
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Какие из следующих трёх векторов компланарны: а) \(\vec{AA_1}\), \(\vec{CC_1}\), \(\vec{BB_1}\); б) \(\vec{АВ}\), \(\vec{AD}\), \(\vec{AA_1}\); в) \(\vec{B_1B}\), \(\vec{АС}\), \(\vec{DD_1}\); г) \(\vec{AD}\), \(\vec{CC_1}\), \(\vec{A_1B}\)?
Векторы \(\vec{AA_1}\), \(\vec{BB_1}\), и \(\vec{CC_1}\) коллинеарны, так как они параллельны и равны по длине как боковые ребра параллелепипеда. Коллинеарные векторы всегда компланарны. Векторы \(\vec{B_1B}\), \(\vec{АС}\), и \(\vec{DD_1}\) компланарны, так как вектор \(\vec{DD_1}\) равен вектору \(\vec{AA_1}\), а вектор \(\vec{B_1B}\) равен вектору \(\vec{C_1C}\), и векторы \(\vec{AA_1}\), \(\vec{AC}\), и \(\vec{C_1C}\) лежат в одной плоскости \(AA_1C_1C\).
Рассмотрим каждый набор векторов отдельно, чтобы определить, являются ли они компланарными. Векторы называются компланарными, если при откладывании их от одной точки они лежат в одной плоскости.
Для случая а) даны векторы \(\vec{AA_1}\), \(\vec{BB_1}\), и \(\vec{CC_1}\). В параллелепипеде боковые ребра, соединяющие соответствующие вершины оснований, параллельны и равны по длине. Следовательно, векторы \(\vec{AA_1}\), \(\vec{BB_1}\), и \(\vec{CC_1}\) являются коллинеарными, так как они параллельны друг другу (\(\vec{AA_1} \parallel \vec{BB_1} \parallel \vec{CC_1}\)). Коллинеарные векторы по определению лежат на одной прямой или на параллельных прямых. Если отложить коллинеарные векторы от одной точки, они будут лежать на одной прямой, а любая прямая лежит в плоскости. Таким образом, векторы \(\vec{AA_1}\), \(\vec{BB_1}\), и \(\vec{CC_1}\) компланарны.
Для случая б) даны векторы \(\vec{AB}\), \(\vec{AD}\), и \(\vec{AA_1}\). Эти три вектора выходят из одной вершины A и определяют рёбра параллелепипеда, исходящие из этой вершины. Векторы \(\vec{AB}\) и \(\vec{AD}\) лежат в плоскости нижнего основания \(ABCD\). Вектор \(\vec{AA_1}\) перпендикулярен плоскости основания \(ABCD\) (в случае прямого параллелепипеда) или просто не лежит в этой плоскости (в случае наклонного параллелепипеда), если только параллелепипед не является вырожденным. Поскольку вектор \(\vec{AA_1}\) не лежит в плоскости, определяемой векторами \(\vec{AB}\) и \(\vec{AD}\), эти три вектора, выходящие из одной точки А, не лежат в одной плоскости. Следовательно, векторы \(\vec{AB}\), \(\vec{AD}\), и \(\vec{AA_1}\) не компланарны.
Для случая в) даны векторы \(\vec{B_1B}\), \(\vec{АС}\), и \(\vec{DD_1}\). Рассмотрим эти векторы. Вектор \(\vec{DD_1}\) является боковым ребром и параллелен вектору \(\vec{AA_1}\) и равен ему по длине, то есть \(\vec{DD_1} = \vec{AA_1}\). Вектор \(\vec{B_1B}\) также является боковым ребром, соединяющим вершины верхнего и нижнего оснований, и он параллелен вектору \(\vec{C_1C}\) и равен ему по длине, но направлен противоположно вектору \(\vec{CC_1}\), то есть \(\vec{B_1B} = -\vec{CC_1}\). Вектор \(\vec{АС}\) является диагональю нижнего основания \(ABCD\). Рассмотрим векторы \(\vec{AA_1}\), \(\vec{AC}\), и \(\vec{C_1C}\). Векторы \(\vec{AA_1}\) и \(\vec{C_1C}\) являются параллельными боковыми ребрами, и они определяют плоскость \(AA_1C_1C\). Вектор \(\vec{AC}\) является диагональю основания \(ABCD\), и прямая AC параллельна прямой \(A_1C_1\), которая лежит в плоскости \(AA_1C_1C\). Следовательно, вектор \(\vec{AC}\) лежит в плоскости \(AA_1C_1C\). Поскольку векторы \(\vec{AA_1}\), \(\vec{AC}\), и \(\vec{C_1C}\) лежат в одной плоскости \(AA_1C_1C\), а векторы \(\vec{DD_1}\) и \(\vec{B_1B}\) параллельны векторам \(\vec{AA_1}\) и \(\vec{C_1C}\) соответственно (с учетом направления), то векторы \(\vec{B_1B}\), \(\vec{АС}\), и \(\vec{DD_1}\) компланарны.
Для случая г) даны векторы \(\vec{AD}\), \(\vec{CC_1}\), и \(\vec{A_1B}\). Вектор \(\vec{AD}\) лежит в плоскости нижнего основания \(ABCD\). Вектор \(\vec{CC_1}\) параллелен вектору \(\vec{AA_1}\). Вектор \(\vec{A_1B}\) является диагональю боковой грани \(A_1ABB_1\). Отложим все векторы от одной точки, например, от точки А. Вектор \(\vec{AD}\) остается вектором \(\vec{AD}\). Вектор \(\vec{CC_1}\) при откладывании от точки А равен вектору \(\vec{AA_1}\). Вектор \(\vec{A_1B}\) при откладывании от точки А равен \(\vec{AB} — \vec{AA_1}\). Таким образом, мы имеем три вектора, выходящие из точки А: \(\vec{AD}\), \(\vec{AA_1}\), и \(\vec{AB} — \vec{AA_1}\). Векторы \(\vec{AD}\) и \(\vec{AA_1}\) определяют плоскость боковой грани \(AA_1D_1D\). Вектор \(\vec{AB} — \vec{AA_1}\) представляет собой вектор \(\vec{A_1B}\). Этот вектор не лежит в плоскости \(AA_1D_1D\), если только параллелепипед не является вырожденным. Следовательно, векторы \(\vec{AD}\), \(\vec{CC_1}\), и \(\vec{A_1B}\) не компланарны.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.