ГДЗ по Геометрии 11 класс Номер 587 Атанасян — Подробные Ответы

Известно, что \(|\vec{p}| = |\vec{a} + \vec{b} + \vec{c}|\), причём векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) попарно не сонаправлены. Докажите, что \(|\vec{p}| = |\vec{a}| + |\vec{b}| + |\vec{c}|\).

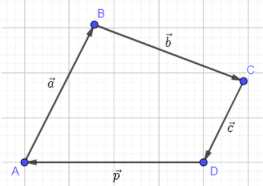
Пусть \(\vec{AB} = \vec{a}\), \(\vec{BC} = \vec{b}\), \(\vec{CD} = \vec{c}\). Тогда сумма векторов \(\vec{a} + \vec{b} + \vec{c}\) равна вектору \(\vec{AD}\), то есть \(\vec{p} = \vec{AD}\). Поскольку векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) попарно не сонаправлены, точки A, B, C и D не лежат на одной прямой и образуют четырехугольник ABCD. Из неравенства многоугольника следует, что длина стороны AD меньше суммы длин сторон AB, BC и CD, то есть \(|\vec{AD}| < |\vec{AB}| + |\vec{BC}| + |\vec{CD}|\). Подставляя соответствующие векторы, получаем \(|\vec{p}| < |\vec{a}| + |\vec{b}| + |\vec{c}|\), что и требовалось доказать.

Дано: векторы \(\vec{a}\), \(\vec{b}\), \(\vec{c}\), \(\vec{p}\) такие, что \(\vec{p} = \vec{a} + \vec{b} + \vec{c}\). Также известно, что векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) попарно не сонаправлены. Требуется доказать неравенство \(|\vec{p}| < |\vec{a}| + |\vec{b}| + |\vec{c}|\). Для доказательства воспользуемся геометрическим представлением сложения векторов. Векторы можно перемещать параллельно самим себе так, чтобы начало одного вектора совпадало с концом другого. Пусть точка A является началом вектора \(\vec{a}\). Отложим от точки A вектор \(\vec{AB} = \vec{a}\). Затем от конца вектора \(\vec{AB}\), то есть от точки B, отложим вектор \(\vec{BC} = \vec{b}\). Далее от конца вектора \(\vec{BC}\), то есть от точки C, отложим вектор \(\vec{CD} = \vec{c}\). Согласно правилу сложения векторов, сумма векторов \(\vec{AB} + \vec{BC} + \vec{CD}\) равна вектору, идущему из начала первого вектора (точки A) в конец последнего вектора (точки D). Таким образом, \(\vec{AD} = \vec{AB} + \vec{BC} + \vec{CD}\). По условию задачи, \(\vec{p} = \vec{a} + \vec{b} + \vec{c}\). Подставляя наши обозначения, получаем \(\vec{p} = \vec{AB} + \vec{BC} + \vec{CD}\). Следовательно, \(\vec{AD} = \vec{p}\). Поскольку векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) попарно не сонаправлены, точки A, B, C и D не лежат на одной прямой. Если бы, например, \(\vec{a}\) и \(\vec{b}\) были сонаправлены, то точки A, B, C могли бы лежать на одной прямой. Если бы \(\vec{a} + \vec{b}\) и \(\vec{c}\) были сонаправлены, то точки A, C, D могли бы лежать на одной прямой. Условие попарной несонаправленности гарантирует, что точки A, B, C, D образуют невырожденный четырехугольник ABCD. Для любого многоугольника (в данном случае четырехугольника ABCD) длина одной стороны всегда меньше или равна сумме длин остальных сторон. Это утверждение является обобщением неравенства треугольника. Для нашего четырехугольника ABCD справедливо неравенство: длина стороны AD меньше суммы длин сторон AB, BC и CD. В символьной записи это выглядит так: \(|\vec{AD}| \le |\vec{AB}| + |\vec{BC}| + |\vec{CD}|\). Так как точки A, B, C, D не лежат на одной прямой (из-за попарной несонаправленности векторов \(\vec{a}\), \(\vec{b}\), \(\vec{c}\)), четырехугольник ABCD не является вырожденным. В невырожденном многоугольнике длина одной стороны строго меньше суммы длин остальных сторон. Поэтому мы можем использовать строгое неравенство: \(|\vec{AD}| < |\vec{AB}| + |\vec{BC}| + |\vec{CD}|\). Подставляя обратно векторы, соответствующие сторонам, получаем: \(|\vec{p}| < |\vec{a}| + |\vec{b}| + |\vec{c}|\). Таким образом, мы доказали, что длина вектора \(\vec{p}\) строго меньше суммы длин векторов \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\), что и требовалось доказать.