Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 586 Атанасян — Подробные Ответы
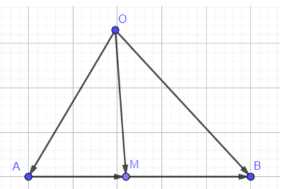
Три точки \(А\), \(В\) и \(М\) удовлетворяют условию \(\vec{АМ} = \lambda \cdot \vec{МВ}\), где \(\lambda \neq -1\). Докажите, что эти точки лежат на одной прямой и для любой точки \(О\) пространства выполняется равенство \(\vec{ОМ} = \frac{\vec{ОА} + \lambda \cdot \vec{ОВ}}{1 + \lambda}\).
Решение
Из равенства \(\vec{АМ} = \lambda \cdot \vec{МВ}\) следует, что векторы \(\vec{АМ}\) и \(\vec{МВ}\) коллинеарны, поэтому прямые \(АМ\) и \(МВ\) либо параллельны, либо совпадают. Так как эти прямые имеют общую точку \(М\), то они совпадают, и, следовательно, точки \(А\), \(В\) и \(М\) лежат на одной прямой. Поскольку \(\vec{АМ} = \vec{ОМ} — \vec{ОА}\), \(\vec{МВ} = \vec{ОВ} — \vec{ОМ}\), то из равенства \(\vec{АМ} = \lambda \cdot \vec{МВ}\) имеем \(\vec{ОМ} — \vec{ОА} = \lambda(\vec{ОВ} — \vec{ОМ})\), или \((1 + \lambda)\vec{ОМ} = \vec{ОА} + \lambda \cdot \vec{ОВ}\). Отсюда, разделив на \(1 + \lambda\), получаем искомое равенство.
Три точки \(А\), \(В\), \(М\) удовлетворяют условию \(\vec{АМ} = \lambda \cdot \vec{МВ}\), \(\lambda \neq -1\). Из этого следует, что векторы \(\vec{АМ}\) и \(\vec{МВ}\) коллинеарны, а поскольку у них есть общая точка \(М\), то точки \(А\), \(В\) и \(М\) лежат на одной прямой. Используя формулы для векторов \(\vec{АМ} = \vec{ОМ} — \vec{ОА}\) и \(\vec{МВ} = \vec{ОВ} — \vec{ОМ}\), подставим их в исходное равенство: \(\vec{ОМ} — \vec{ОА} = \lambda(\vec{ОВ} — \vec{ОМ})\). Раскрывая скобки и группируя члены с \(\vec{ОМ}\), получаем \((1 + \lambda)\vec{ОМ} = \vec{ОА} + \lambda \cdot \vec{ОВ}\). Разделив обе части на \((1 + \lambda)\) (что возможно, так как \(\lambda \neq -1\)), получаем \(\vec{ОМ} = \frac{\vec{ОА} + \lambda \cdot \vec{ОВ}}{1 + \lambda}\), что и требовалось доказать.
Дано: Три точки \(А\), \(В\), \(М\) и равенство \(\vec{АМ} = \lambda \cdot \vec{МВ}\), где \(\lambda \neq -1\).
Требуется доказать, что точки \(А\), \(В\), \(М\) лежат на одной прямой и что для любой точки \(О\) пространства справедливо равенство \(\vec{ОМ} = \frac{\vec{ОА} + \lambda \cdot \vec{ОВ}}{1 + \lambda}\).
Доказательство:
Из данного равенства \(\vec{АМ} = \lambda \cdot \vec{МВ}\) следует, что вектор \(\vec{АМ}\) является произведением скаляра \(\lambda\) на вектор \(\vec{МВ}\). По определению коллинеарных векторов, это означает, что векторы \(\vec{АМ}\) и \(\vec{МВ}\) коллинеарны. Коллинеарные векторы лежат либо на параллельных прямых, либо на одной прямой. Таким образом, прямые \(АМ\) и \(МВ\) либо параллельны, либо совпадают.
Далее, поскольку прямые \(АМ\) и \(МВ\) имеют общую точку \(М\), они не могут быть параллельными. Следовательно, эти прямые совпадают. Если точки \(А\), \(М\) лежат на прямой \(АМ\), и точки \(М\), \(В\) лежат на прямой \(МВ\), а прямые \(АМ\) и \(МВ\) совпадают, то все три точки \(А\), \(В\), \(М\) лежат на одной прямой. Это завершает первую часть доказательства.
Теперь докажем вторую часть равенства для любой точки \(О\) пространства. Вектор \(\vec{АМ}\) может быть выражен как разность радиус-вектора точки \(М\) и радиус-вектора точки \(А\) относительно точки \(О\), то есть \(\vec{АМ} = \vec{ОМ} — \vec{ОА}\). Аналогично, вектор \(\vec{МВ}\) может быть выражен как разность радиус-вектора точки \(В\) и радиус-вектора точки \(М\) относительно точки \(О\), то есть \(\vec{МВ} = \vec{ОВ} — \vec{ОМ}\).
Подставим эти выражения для \(\vec{АМ}\) и \(\vec{МВ}\) в исходное равенство \(\vec{АМ} = \lambda \cdot \vec{МВ}\):
\(\vec{ОМ} — \vec{ОА} = \lambda \cdot (\vec{ОВ} — \vec{ОМ})\).
Раскроем скобки в правой части уравнения:
\(\vec{ОМ} — \vec{ОА} = \lambda \cdot \vec{ОВ} — \lambda \cdot \vec{ОМ}\).
Теперь соберем все члены, содержащие \(\vec{ОМ}\), в одной части уравнения, а остальные члены — в другой. Перенесем член \(-\lambda \cdot \vec{ОМ}\) из правой части в левую, изменив знак, и член \(-\vec{ОА}\) из левой части в правую, также изменив знак:
\(\vec{ОМ} + \lambda \cdot \vec{ОМ} = \vec{ОА} + \lambda \cdot \vec{ОВ}\).
Вынесем общий множитель \(\vec{ОМ}\) в левой части:
\((1 + \lambda)\vec{ОМ} = \vec{ОА} + \lambda \cdot \vec{ОВ}\).
По условию дано, что \(\lambda \neq -1\), следовательно, \(1 + \lambda \neq 0\). Мы можем разделить обе части уравнения на скаляр \((1 + \lambda)\):
\(\vec{ОМ} = \frac{\vec{ОА} + \lambda \cdot \vec{ОВ}}{1 + \lambda}\).
Таким образом, мы получили требуемое равенство, что завершает доказательство.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.