
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 585 Атанасян — Подробные Ответы
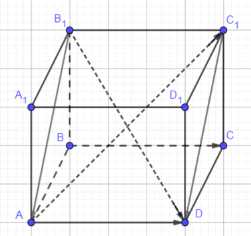
Докажите, что в параллелепипеде \(ABCDA_1B_1C_1D_1\) \(\vec{AC_1} + \vec{B_1D} = 2\vec{ВС}\).
В параллелепипеде \(ABCDA_1B_1C_1D_1\) имеем \(\vec{AD} = \vec{BC}\) и \(\vec{B_1A} = \vec{C_1D} = -\vec{DC_1}\).
Вектор \(\vec{B_1D}\) можно представить как сумму векторов \(\vec{B_1A} + \vec{AD}\).
Вектор \(\vec{AC_1}\) можно представить как сумму векторов \(\vec{AD} + \vec{DC_1}\).
Складывая эти выражения, получаем \(\vec{AC_1} + \vec{B_1D} = (\vec{AD} + \vec{DC_1}) + (\vec{B_1A} + \vec{AD})\).
Перегруппируем и используем свойства параллелепипеда: \(\vec{AC_1} + \vec{B_1D} = 2\vec{AD} + \vec{DC_1} + \vec{B_1A} = 2\vec{BC} + \vec{DC_1} + (-\vec{DC_1}) = 2\vec{BC}\).
Таким образом, \(\vec{AC_1} + \vec{B_1D} = 2\vec{BC}\), что и требовалось доказать.
Рассмотрим параллелепипед \(ABCDA_1B_1C_1D_1\). По определению параллелепипеда, его противоположные грани параллельны и равны, что влечет равенство и параллельность соответствующих ребер. Векторы, направленные вдоль параллельных и равных отрезков в одном направлении, равны. Векторы, направленные вдоль параллельных и равных отрезков в противоположных направлениях, противоположны.
В данном параллелепипеде ребра \(AD\) и \(BC\) параллельны и равны по длине, а также направлены в одну сторону, следовательно, вектор \(\vec{AD}\) равен вектору \(\vec{BC}\), то есть \(\vec{AD} = \vec{BC}\).
Ребра \(B_1A\) и \(C_1D\) также параллельны и равны по длине. Если мы рассмотрим направление от \(B_1\) к \(A\) и от \(C_1\) к \(D\), эти векторы будут равны: \(\vec{B_1A} = \vec{C_1D}\). Вектор \(\vec{DC_1}\) направлен от \(D\) к \(C_1\). Поскольку \(C_1D\) и \(DC_1\) лежат на одной прямой и имеют одинаковую длину, но противоположные направления, вектор \(\vec{C_1D}\) противоположен вектору \(\vec{DC_1}\), то есть \(\vec{C_1D} = -\vec{DC_1}\). Отсюда следует, что \(\vec{B_1A} = \vec{C_1D} = -\vec{DC_1}\).
Теперь выразим векторы \(\vec{B_1D}\) и \(\vec{AC_1}\) через другие векторы, используя правило сложения векторов (правило треугольника или многоугольника).
Вектор \(\vec{B_1D}\) можно представить как сумму векторов \(\vec{B_1A}\) и \(\vec{AD}\): \(\vec{B_1D} = \vec{B_1A} + \vec{AD}\). Это следует из рассмотрения треугольника \(B_1AD\).
Вектор \(\vec{AC_1}\) можно представить как сумму векторов \(\vec{AD}\) и \(\vec{DC_1}\): \(\vec{AC_1} = \vec{AD} + \vec{DC_1}\). Это следует из рассмотрения ломаной \(ADC_1\).
Сложим полученные векторные равенства для \(\vec{AC_1}\) и \(\vec{B_1D}\):
\(\vec{AC_1} + \vec{B_1D} = (\vec{AD} + \vec{DC_1}) + (\vec{B_1A} + \vec{AD})\).
Перегруппируем слагаемые в правой части равенства:
\(\vec{AC_1} + \vec{B_1D} = \vec{AD} + \vec{AD} + \vec{DC_1} + \vec{B_1A}\).
Сумма двух одинаковых векторов равна удвоенному вектору: \(\vec{AD} + \vec{AD} = 2\vec{AD}\).
Таким образом, \(\vec{AC_1} + \vec{B_1D} = 2\vec{AD} + \vec{DC_1} + \vec{B_1A}\).
Теперь подставим в это выражение равенства, установленные в начале доказательства: \(\vec{AD} = \vec{BC}\) и \(\vec{B_1A} = -\vec{DC_1}\).
\(\vec{AC_1} + \vec{B_1D} = 2\vec{BC} + \vec{DC_1} + (-\vec{DC_1})\).
Вектор \(\vec{DC_1}\) и вектор \(-\vec{DC_1}\) являются противоположными векторами, их сумма равна нулевому вектору: \(\vec{DC_1} + (-\vec{DC_1}) = \vec{0}\).
Следовательно, \(\vec{AC_1} + \vec{B_1D} = 2\vec{BC} + \vec{0} = 2\vec{BC}\).
Мы получили равенство \(\vec{AC_1} + \vec{B_1D} = 2\vec{BC}\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!