
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 583 Атанасян — Подробные Ответы
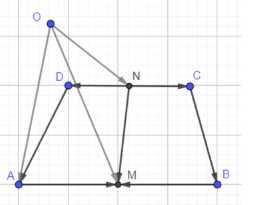
Точки \(М\) и \(N\) — середины сторон \(AB\) и \(CD\) трапеции \(ABCD\), а \(О\) — произвольная точка пространства. Выразите вектор \(\vec{ОМ} — \vec{ON}\) через векторы \(\vec{AD}\) и \(\vec{ВС}\).
Вектор \(\vec{ON}\) можно выразить как \(\vec{OA} + \vec{AD} + \vec{DN}\), а вектор \(\vec{OM}\) как \(\vec{OA} + \vec{AM}\). Тогда разность векторов \(\vec{OM} — \vec{ON}\) равна \((\vec{OA} + \vec{AM}) — (\vec{OA} + \vec{AD} + \vec{DN}) = \vec{AM} — \vec{AD} — \vec{DN}\). Перегруппируя с учетом изменения направления векторов, получаем \(\vec{AM} + \vec{DA} + \vec{ND}\), что по правилу сложения векторов равно \(\vec{NM}\). Таким образом, \(\vec{OM} — \vec{ON} = \vec{NM}\).
Вектор \(\vec{NM}\) также можно представить как \(\vec{NC} + \vec{CB} + \vec{BM}\).
Складывая два выражения для \(\vec{NM}\), получаем \(2\vec{NM} = (\vec{ND} + \vec{DA} + \vec{AM}) + (\vec{NC} + \vec{CB} + \vec{BM})\).
Поскольку \(M\) и \(N\) являются серединами сторон \(AB\) и \(CD\) соответственно, имеем \(\vec{AM} = -\vec{BM}\) и \(\vec{ND} = -\vec{NC}\). Подставляя это в сумму, получаем \(2\vec{NM} = (\vec{ND} + \vec{NC}) + \vec{DA} + \vec{CB} + (\vec{AM} + \vec{BM}) = \vec{0} + \vec{DA} + \vec{CB} + \vec{0} =\)
\(= \vec{DA} + \vec{CB}\).
Известно, что \(\vec{DA} = -\vec{AD}\) и \(\vec{CB} = -\vec{BC}\). Подставляя это в выражение для \(2\vec{NM}\), получаем \(2\vec{NM} = -\vec{AD} — \vec{BC}\).
Следовательно, \(\vec{NM} = -\frac{1}{2}(\vec{AD} + \vec{BC})\).
Так как \(\vec{OM} — \vec{ON} = \vec{NM}\), окончательно получаем \(\vec{OM} — \vec{ON} = -\frac{1}{2}(\vec{AD} + \vec{BC})\).
Начнем с выражения векторов \(\vec{ON}\) и \(\vec{OM}\) через радиус-векторы точек относительно произвольной точки \(O\). Вектор \(\vec{ON}\) можно представить как сумму векторов \(\vec{OA}\), \(\vec{AD}\) и \(\vec{DN}\), то есть \(\vec{ON} = \vec{OA} + \vec{AD} + \vec{DN}\). Аналогично, вектор \(\vec{OM}\) можно представить как сумму векторов \(\vec{OA}\) и \(\vec{AM}\), то есть \(\vec{OM} = \vec{OA} + \vec{AM}\).
Теперь найдем разность векторов \(\vec{OM} — \vec{ON}\). Подставляя полученные выражения, имеем \(\vec{OM} — \vec{ON} = (\vec{OA} + \vec{AM}) — (\vec{OA} + \vec{AD} + \vec{DN})\). Раскрывая скобки и меняя знаки у вычитаемых векторов, получаем \(\vec{OM} — \vec{ON} = \vec{OA} + \vec{AM} — \vec{OA} — \vec{AD} — \vec{DN}\). Векторы \(\vec{OA}\) и \(-\vec{OA}\) взаимно уничтожаются, остаётся \(\vec{OM} — \vec{ON} = \vec{AM} — \vec{AD} — \vec{DN}\). Переставляя слагаемые и учитывая, что \(\vec{DA} = -\vec{AD}\) и \(\vec{ND} = -\vec{DN}\), мы можем записать \(\vec{OM} — \vec{ON} = \vec{AM} + \vec{DA} + \vec{ND}\). По правилу сложения векторов, сумма \(\vec{ND} + \vec{DA} + \vec{AM}\) представляет собой вектор, идущий из начальной точки вектора \(\vec{ND}\) в конечную точку вектора \(\vec{AM}\), то есть вектор \(\vec{NM}\). Таким образом, мы установили, что \(\vec{OM} — \vec{ON} = \vec{NM}\).
Теперь выразим вектор \(\vec{NM}\) другим способом. Мы можем пройти из точки \(N\) в точку \(M\) через точки \(C\) и \(B\). В этом случае \(\vec{NM} = \vec{NC} + \vec{CB} + \vec{BM}\).
У нас есть два выражения для вектора \(\vec{NM}\): \(\vec{NM} = \vec{ND} + \vec{DA} + \vec{AM}\) и \(\vec{NM} = \vec{NC} + \vec{CB} + \vec{BM}\). Сложим эти два равенства: \(2\vec{NM} = (\vec{ND} + \vec{DA} + \vec{AM}) + (\vec{NC} + \vec{CB} + \vec{BM})\).
По условию, \(M\) является серединой отрезка \(AB\), что означает, что вектор \(\vec{AM}\) противоположен вектору \(\vec{BM}\) по направлению и равен ему по длине, то есть \(\vec{AM} = -\vec{BM}\). Аналогично, \(N\) является серединой отрезка \(CD\), что означает, что вектор \(\vec{DN}\) противоположен вектору \(\vec{CN}\), или \(\vec{ND} = -\vec{NC}\).
Подставим эти соотношения в сумму векторов: \(2\vec{NM} = (\vec{ND} + \vec{DA} + \vec{AM}) + (-\vec{ND} + \vec{CB} — \vec{AM})\). Перегруппируем слагаемые: \(2\vec{NM} = (\vec{ND} — \vec{ND}) + \vec{DA} + \vec{CB} + (\vec{AM} — \vec{AM})\). Векторы \(\vec{ND}\) и \(-\vec{ND}\) взаимно уничтожаются, так же как и \(\vec{AM}\) и \(-\vec{AM}\). Получаем \(2\vec{NM} = \vec{DA} + \vec{CB}\).
Теперь выразим векторы \(\vec{DA}\) и \(\vec{CB}\) через векторы \(\vec{AD}\) и \(\vec{BC}\). Вектор \(\vec{DA}\) противоположен вектору \(\vec{AD}\), поэтому \(\vec{DA} = -\vec{AD}\). Аналогично, вектор \(\vec{CB}\) противоположен вектору \(\vec{BC}\), поэтому \(\vec{CB} = -\vec{BC}\).
Подставим эти выражения в равенство для \(2\vec{NM}\): \(2\vec{NM} = -\vec{AD} — \vec{BC}\).
Разделим обе части на 2, чтобы найти вектор \(\vec{NM}\): \(\vec{NM} = -\frac{1}{2}(\vec{AD} + \vec{BC})\).
Поскольку ранее мы установили, что \(\vec{OM} — \vec{ON} = \vec{NM}\), мы можем заключить, что \(\vec{OM} — \vec{ON} = -\frac{1}{2}(\vec{AD} + \vec{BC})\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!