Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 582 Атанасян — Подробные Ответы
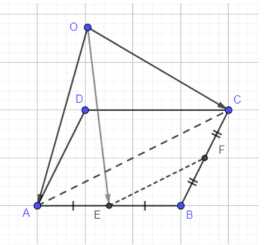
Точки \(E\) и \(F\) — середины оснований \(АВ\) и \(ВС\) параллелограмма \(ABCD\), а \(О\) — произвольная точка пространства. Выразите: а) вектор \(\vec{ОА} — \vec{ОС}\) через вектор \(\vec{EF}\); б) вектор \(\vec{ОА} — \vec{ОВ}\) через вектор \(\vec{DC}\).
Дано: \(ABCD\) — параллелограмм; \(АЕ = ЕВ\); \(BF = FC\); \(О\) — произвольная точка пространства; Выразить: а) вектор \(\vec{ОА} — \vec{ОС}\) через \(\vec{EF}\); б) вектор \(\vec{ОА} — \vec{ОЕ}\) через \(\vec{DC}\).
Решение:
а) \(\vec{ОС} = \vec{ОА} + \vec{АС}\), тогда \(\vec{ОА} — \vec{ОС} = \vec{ОА} — (\vec{ОА} + \vec{АС}) = -\vec{АС}\). Точки \(Е\) и \(F\) середины сторон \(АВ\) и \(ВС\), значит в \(\triangle АВС\): \(EF\) — средняя линия, тогда \(\vec{EF} = \frac{1}{2}\vec{АС}\), отсюда \(-\vec{АС} = -2\vec{EF}\).
б) \(\vec{ОА} = \vec{ОЕ} + \vec{ЕА}\), тогда \(\vec{ОА} — \vec{ОЕ} = \vec{ОЕ} + \vec{ЕА} — \vec{ОЕ} = \vec{ЕА}\). \(АЕ = ЕВ\) (так как \(Е\) — середина \(АВ\)) и \(\vec{АВ} = \vec{DC}\) (по свойству параллелограмма), значит \(\vec{ЕА} = -\vec{АЕ}\). Так как \(Е\) середина \(АВ\), \(\vec{АЕ} = \frac{1}{2}\vec{АВ}\). Следовательно \(\vec{ЕА} = -\frac{1}{2}\vec{АВ}\). Поскольку \(\vec{АВ} = \vec{DC}\), \(\vec{ЕА} = -\frac{1}{2}\vec{DC}\).
Ответ: а) \(-2\vec{EF}\); б) \(-\frac{1}{2}\vec{DC}\).
Дано: \(ABCD\) — параллелограмм; \(АЕ = ЕВ\); \(BF = FC\); \(О\) — произвольная точка пространства; Выразить: а) вектор \(\vec{ОА} — \vec{ОС}\) через \(\vec{EF}\); б) вектор \(\vec{ОА} — \vec{ОЕ}\) через \(\vec{DC}\).
Решение:
а) Выразим вектор \(\vec{ОА} — \vec{ОС}\) через \(\vec{EF}\).
Используем правило вычитания векторов, которое гласит, что \(\vec{ОА} — \vec{ОС} = \vec{СА}\).
Альтернативно, можно выразить вектор \(\vec{ОС}\) через \(\vec{ОА}\) и \(\vec{АС}\), используя правило сложения векторов: \(\vec{ОС} = \vec{ОА} + \vec{АС}\).
Тогда разность векторов \(\vec{ОА} — \vec{ОС}\) будет равна:
\(\vec{ОА} — \vec{ОС} = \vec{ОА} — (\vec{ОА} + \vec{АС})\)
Раскрывая скобки, получаем:
\(\vec{ОА} — \vec{ОС} = \vec{ОА} — \vec{ОА} — \vec{АС}\)
\(\vec{ОА} — \vec{ОС} = \vec{0} — \vec{АС}\)
\(\vec{ОА} — \vec{ОС} = -\vec{АС}\)
Теперь необходимо выразить вектор \(\vec{АС}\) через вектор \(\vec{EF}\).
По условию, точка \(Е\) является серединой стороны \(АВ\), а точка \(F\) является серединой стороны \(ВС\) параллелограмма \(ABCD\).
Рассмотрим треугольник \(АВС\). Отрезок \(EF\) соединяет середину стороны \(АВ\) (\(Е\)) и середину стороны \(ВС\) (\(F\)).
По теореме о средней линии треугольника, средняя линия \(EF\) параллельна третьей стороне \(АС\) и ее длина равна половине длины этой стороны.
В векторной форме это означает, что вектор \(\vec{EF}\) сонаправлен с вектором \(\vec{АС}\) и его длина равна половине длины вектора \(\vec{АС}\).
Следовательно, вектор \(\vec{EF}\) равен половине вектора \(\vec{АС}\):
\(\vec{EF} = \frac{1}{2}\vec{АС}\)
Чтобы выразить \(\vec{АС}\) через \(\vec{EF}\), умножим обе части уравнения на 2:
\(2\vec{EF} = \vec{АС}\)
Теперь подставим это выражение для \(\vec{АС}\) в формулу для \(\vec{ОА} — \vec{ОС}\):
\(\vec{ОА} — \vec{ОС} = -\vec{АС}\)
\(\vec{ОА} — \vec{ОС} = -(2\vec{EF})\)
\(\vec{ОА} — \vec{ОС} = -2\vec{EF}\)
б) Выразим вектор \(\vec{ОА} — \vec{ОЕ}\) через \(\vec{DC}\).
Используем правило вычитания векторов: \(\vec{ОА} — \vec{ОЕ} = \vec{ЕА}\).
Альтернативно, можно выразить вектор \(\vec{ОА}\) через \(\vec{ОЕ}\) и \(\vec{ЕА}\), используя правило сложения векторов: \(\vec{ОА} = \vec{ОЕ} + \vec{ЕА}\).
Тогда разность векторов \(\vec{ОА} — \vec{ОЕ}\) будет равна:
\(\vec{ОА} — \vec{ОЕ} = (\vec{ОЕ} + \vec{ЕА}) — \vec{ОЕ}\)
Раскрывая скобки, получаем:
\(\vec{ОА} — \vec{ОЕ} = \vec{ОЕ} + \vec{ЕА} — \vec{ОЕ}\)
\(\vec{ОА} — \vec{ОЕ} = \vec{ЕА}\)
Теперь необходимо выразить вектор \(\vec{ЕА}\) через вектор \(\vec{DC}\).
По условию, точка \(Е\) является серединой стороны \(АВ\). Это означает, что вектор \(\vec{АЕ}\) равен половине вектора \(\vec{АВ}\) и сонаправлен с ним:
\(\vec{АЕ} = \frac{1}{2}\vec{АВ}\)
Вектор \(\vec{ЕА}\) является противоположным вектору \(\vec{АЕ}\), то есть:
\(\vec{ЕА} = -\vec{АЕ}\)
Подставим выражение для \(\vec{АЕ}\):
\(\vec{ЕА} = -(\frac{1}{2}\vec{АВ})\)
\(\vec{ЕА} = -\frac{1}{2}\vec{АВ}\)
Поскольку \(ABCD\) — параллелограмм, противоположные стороны \(АВ\) и \(DC\) параллельны и равны по длине. Векторы, направленные вдоль этих сторон в одном направлении, равны. Таким образом, вектор \(\vec{АВ}\) равен вектору \(\vec{DC}\):
\(\vec{АВ} = \vec{DC}\)
Теперь подставим это равенство в выражение для \(\vec{ЕА}\):
\(\vec{ЕА} = -\frac{1}{2}\vec{АВ}\)
\(\vec{ЕА} = -\frac{1}{2}\vec{DC}\)
Следовательно, \(\vec{ОА} — \vec{ОЕ} = \vec{ЕА} = -\frac{1}{2}\vec{DC}\).
Ответ: а) \(-2\vec{EF}\); б) \(-\frac{1}{2}\vec{DC}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.