
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 581 Атанасян — Подробные Ответы
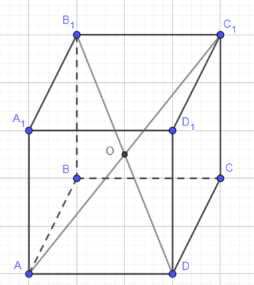
Диагонали куба \(ABCDA_1B_1C_1D_1\) пересекаются в точке \(О\). Найдите число \(k\), такое, что: а) \(\vec{АВ} = k \cdot \vec{CD}\); б) \(\vec{АС_1} = k \cdot \vec{АО}\); в) \(\vec{ОВ_1} = k \cdot \vec{B_1D}\).
а) \(\vec{АВ} = k \cdot \vec{CD}\). Так как \(\vec{АВ}\) и \(\vec{CD}\) противоположно направлены и равны по длине, \(\vec{АВ} = -\vec{CD}\). Следовательно, \(-\vec{CD} = k \cdot \vec{CD}\), откуда \(k = -1\).
б) \(\vec{АС_1} = k \cdot \vec{АО}\). Точка \(О\) является серединой диагонали \(АС_1\), поэтому \(\vec{АС_1} = 2 \cdot \vec{АО}\). Следовательно, \(2 \cdot \vec{АО} = k \cdot \vec{АО}\), откуда \(k = 2\).
в) \(\vec{ОВ_1} = k \cdot \vec{B_1D}\). Точка \(О\) является серединой диагонали \(B_1D\), поэтому \(\vec{ОВ_1} = -\frac{1}{2} \vec{B_1D}\). Следовательно, \(-\frac{1}{2} \vec{B_1D} = k \cdot \vec{B_1D}\), откуда \(k = -\frac{1}{2}\).
Для решения данной задачи рассмотрим куб \(ABCDA_1B_1C_1D_1\). Точка \(О\) является точкой пересечения диагоналей \(АС_1\) и \(BD_1\), что означает, что \(О\) является центром куба. Центр куба делит пополам все пространственные диагонали.
а) Нам дано векторное равенство \(\vec{АВ} = k \cdot \vec{CD}\). В кубе ребра \(АВ\) и \(CD\) являются противоположными ребрами. Они параллельны друг другу и имеют одинаковую длину. Однако, векторы \(\vec{АВ}\) и \(\vec{CD}\) направлены в противоположные стороны (если смотреть вдоль направления обхода вершин основания). Следовательно, вектор \(\vec{АВ}\) равен вектору \(\vec{CD}\) по модулю, но противоположен по направлению. Это можно записать как \(\vec{АВ} = -\vec{CD}\). Подставляя это выражение в исходное равенство, получаем \(-\vec{CD} = k \cdot \vec{CD}\). Поскольку \(\vec{CD}\) является ненулевым вектором (длина ребра куба положительна), мы можем разделить обе части равенства на \(\vec{CD}\), получив \(-1 = k\). Таким образом, значение \(k\) в первом случае равно \(-1\).
б) Нам дано векторное равенство \(\vec{АС_1} = k \cdot \vec{АО}\). Вектор \(\vec{АС_1}\) представляет собой пространственную диагональ куба, соединяющую вершины \(А\) и \(С_1\). Точка \(О\) является центром куба и лежит на этой диагонали. Поскольку \(О\) делит диагональ \(АС_1\) пополам, вектор \(\vec{АО}\) составляет половину вектора \(\vec{АС_1}\) и имеет то же направление. Следовательно, \(\vec{АС_1} = 2 \cdot \vec{АО}\). Подставляя это соотношение в исходное равенство, получаем \(2 \cdot \vec{АО} = k \cdot \vec{АО}\). Поскольку \(\vec{АО}\) является ненулевым вектором, мы можем разделить обе части равенства на \(\vec{АО}\), получив \(2 = k\). Таким образом, значение \(k\) во втором случае равно \(2\).
в) Нам дано векторное равенство \(\vec{ОВ_1} = k \cdot \vec{B_1D}\). Вектор \(\vec{B_1D}\) представляет собой пространственную диагональ куба, соединяющую вершины \(B_1\) и \(D\). Точка \(О\) является центром куба и лежит на этой диагонали, деля ее пополам. Вектор \(\vec{B_1D}\) направлен от вершины \(B_1\) к вершине \(D\). Вектор \(\vec{ОВ_1}\) направлен от центра куба \(О\) к вершине \(B_1\). Поскольку \(О\) является серединой отрезка \(B_1D\), вектор \(\vec{OB_1}\) имеет направление, противоположное вектору \(\vec{OD}\), и равен ему по модулю. Также вектор \(\vec{B_1O}\) равен вектору \(\vec{OD}\). Вектор \(\vec{B_1D}\) можно представить как сумму векторов \(\vec{B_1O}\) и \(\vec{OD}\). Поскольку \(\vec{B_1O} = \vec{OD}\), имеем \(\vec{B_1D} = \vec{B_1O} + \vec{B_1O} = 2 \cdot \vec{B_1O}\). Вектор \(\vec{ОВ_1}\) противоположен вектору \(\vec{B_1O}\), то есть \(\vec{ОВ_1} = -\vec{B_1O}\). Из равенства \(\vec{B_1D} = 2 \cdot \vec{B_1O}\) следует, что \(\vec{B_1O} = \frac{1}{2} \vec{B_1D}\). Подставляем это в выражение для \(\vec{ОВ_1}\): \(\vec{ОВ_1} = -(\frac{1}{2} \vec{B_1D}) = -\frac{1}{2} \vec{B_1D}\). Подставляя это соотношение в исходное равенство \(\vec{ОВ_1} = k \cdot \vec{B_1D}\), получаем \(-\frac{1}{2} \vec{B_1D} = k \cdot \vec{B_1D}\). Поскольку \(\vec{B_1D}\) является ненулевым вектором, мы можем разделить обе части равенства на \(\vec{B_1D}\), получив \(-\frac{1}{2} = k\). Таким образом, значение \(k\) в третьем случае равно \(-\frac{1}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!