Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 580 Атанасян — Подробные Ответы
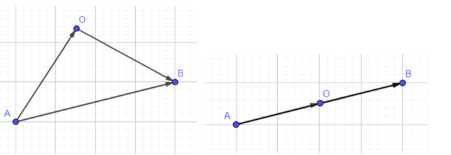
Известно, что \(\vec{АО} = -\frac{1}{2} \vec{АВ}\). Докажите, что точки \(А\) и \(В\) симметричны относительно точки \(О\).
Дано \(\vec{АО} = \frac{1}{2} \vec{АВ}\). Из правила сложения векторов имеем \(\vec{АВ} = \vec{АО} + \vec{ОВ}\). Подставляя данное условие, получаем \(\vec{АВ} = \frac{1}{2} \vec{АВ} + \vec{ОВ}\), откуда следует \(\vec{ОВ} = \vec{АВ} — \frac{1}{2} \vec{АВ} = \frac{1}{2} \vec{АВ}\). Таким образом, \(\vec{АО} = \vec{ОВ}\). Равенство векторов \(\vec{АО}\) и \(\vec{ОВ}\), исходящих из одной точки \(О\), означает, что точки \(А\), \(О\), \(В\) лежат на одной прямой и \(О\) является серединой отрезка \(АВ\). Следовательно, Точки \(А\) и \(В\) симметричны относительно точки \(О\), что и требовалось доказать.
Дано условие, что вектор \(\vec{АО}\) равен половине вектора \(\vec{АВ}\), то есть \(\vec{АО} = \frac{1}{2} \vec{АВ}\). Наша цель состоит в том, чтобы доказать, что точки \(А\) и \(В\) симметричны относительно точки \(О\).
Для начала рассмотрим правило сложения векторов в треугольнике или на прямой. Вектор \(\vec{АВ}\), соединяющий точки \(А\) и \(В\), может быть выражен как сумма векторов \(\vec{АО}\) и \(\vec{ОВ}\), где \(О\) — некоторая промежуточная точка. Таким образом, мы можем записать векторное равенство \(\vec{АВ} = \vec{АО} + \vec{ОВ}\).
Теперь мы можем подставить в это уравнение данное нам условие \(\vec{АО} = \frac{1}{2} \vec{АВ}\). Получаем:
\(\vec{АВ} = \frac{1}{2} \vec{АВ} + \vec{ОВ}\).
Чтобы найти вектор \(\vec{ОВ}\), выразим его из этого уравнения. Перенесем член \(\frac{1}{2} \vec{АВ}\) в левую часть уравнения:
\(\vec{ОВ} = \vec{АВ} — \frac{1}{2} \vec{АВ}\).
Выполняя вычитание векторов, получаем:
\(\vec{ОВ} = \left(1 — \frac{1}{2}\right) \vec{АВ} = \frac{1}{2} \vec{АВ}\).
Итак, мы получили, что \(\vec{ОВ} = \frac{1}{2} \vec{АВ}\). Сравнивая это с исходным условием \(\vec{АО} = \frac{1}{2} \vec{АВ}\), мы видим, что \(\vec{АО} = \vec{ОВ}\).
Равенство двух векторов \(\vec{АО}\) и \(\vec{ОВ}\) означает, что они имеют одинаковую длину и одинаковое направление. Поскольку оба вектора начинаются из точки \(О\), их равенство \(\vec{АО} = \vec{ОВ}\) геометрически интерпретируется следующим образом: точка \(О\) находится на прямой, проходящей через точки \(А\) и \(В\), и расстояние от \(О\) до \(А\) равно расстоянию от \(О\) до \(В\). Более того, векторы \(\vec{ОА}\) (который противоположен \(\vec{АО}\), то есть \(\vec{ОА} = -\vec{АО}\)) и \(\vec{ОВ}\) будут противоположными, поскольку \(\vec{АО} = \vec{ОВ}\) влечет \(\vec{ОА} = -\vec{ОВ}\). Это прямо указывает на то, что точка \(О\) является серединой отрезка \(АВ\).
По определению, две точки \(А\) и \(В\) симметричны относительно точки \(О\), если \(О\) является серединой отрезка \(АВ\). Поскольку мы показали, что \(\vec{АО} = \vec{ОВ}\), точка \(О\) действительно является серединой отрезка \(АВ\).
Следовательно, Точки \(А\) и \(В\) симметричны относительно точки \(О\), что и требовалось доказать.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.