
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 579 Атанасян — Подробные Ответы
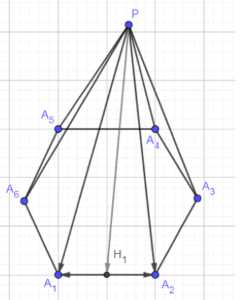
Точка \(Р\) — вершина правильной шестиугольной пирамиды. Докажите, что сумма всех векторов с началом в точке \(Р\), образованных боковыми рёбрами пирамиды, равна сумме всех векторов с началом в точке \(Р\), образованных апофемами.
Пусть \(PH_i\) — апофема грани \(PA_iA_{i+1}\) (где \(A_7=A_1\)). Вектор бокового ребра \(\vec{PA_i}\) можно представить как сумму вектора апофемы и вектора в плоскости основания: \(\vec{PA_i} = \vec{PH_i} + \vec{H_iA_i}\). Аналогично, \(\vec{PA_{i+1}} = \vec{PH_i} + \vec{H_iA_{i+1}}\). Поскольку боковые грани правильной пирамиды являются равными равнобедренными треугольниками, а \(H_i\) — середина ребра \(A_iA_{i+1}\), то \(\vec{H_iA_i} = -\vec{H_iA_{i+1}}\). Сумма векторов боковых рёбер одной грани равна \(\vec{PA_i} + \vec{PA_{i+1}} = (\vec{PH_i} + \vec{H_iA_i}) + (\vec{PH_i} + \vec{H_iA_{i+1}}) = 2\vec{PH_i} + (\vec{H_iA_i} +\)
\(+ \vec{H_iA_{i+1}}) = 2\vec{PH_i} + \vec{0} = 2\vec{PH_i}\). Суммируя это соотношение для всех шести граней, получаем \(\sum_{i=1}^6 (\vec{PA_i} + \vec{PA_{i+1}}) = \sum_{i=1}^6 2\vec{PH_i}\). Левая часть равна \(2\sum_{i=1}^6 \vec{PA_i}\), а правая часть равна \(2\sum_{i=1}^6 \vec{PH_i}\). Следовательно, \(2\sum_{i=1}^6 \vec{PA_i} = 2\sum_{i=1}^6 \vec{PH_i}\), откуда следует \(\sum_{i=1}^6 \vec{PA_i} = \sum_{i=1}^6 \vec{PH_i}\), что и требовалось доказать.
Дана правильная шестиугольная пирамида с вершиной в точке \(P\) и основанием \(A_1A_2A_3A_4A_5A_6\). Требуется доказать, что сумма векторов боковых рёбер, исходящих из вершины \(P\), равна сумме векторов апофем боковых граней, исходящих из вершины \(P\). То есть, необходимо доказать, что \(\sum_{i=1}^6 \vec{PA_i} = \sum_{i=1}^6 \vec{PH_i}\), где \(H_i\) — основание апофемы, опущенной из \(P\) на ребро основания \(A_iA_{i+1}\) (считаем \(A_7 = A_1\)).
Построим апофемы \(PH_i\) для каждой боковой грани пирамиды. Точка \(H_i\) является серединой ребра основания \(A_iA_{i+1}\), поскольку боковые грани правильной пирамиды являются равнобедренными треугольниками (\(PA_i = PA_{i+1}\)), и апофема \(PH_i\) является высотой и медианой в треугольнике \(PA_iA_{i+1}\).
Рассмотрим одну боковую грань, например, \(PA_iA_{i+1}\). Векторы боковых рёбер этой грани, исходящие из \(P\), это \(\vec{PA_i}\) и \(\vec{PA_{i+1}}\). Вектор апофемы этой грани — \(\vec{PH_i}\). Используя правило сложения векторов (правило треугольника), мы можем выразить векторы \(\vec{PA_i}\) и \(\vec{PA_{i+1}}\) через вектор \(\vec{PH_i}\) и векторы \(\vec{H_iA_i}\) и \(\vec{H_iA_{i+1}}\), лежащие на ребре основания \(A_iA_{i+1}\). Получаем:
\(\vec{PA_i} = \vec{PH_i} + \vec{H_iA_i}\)
\(\vec{PA_{i+1}} = \vec{PH_i} + \vec{H_iA_{i+1}}\)
Теперь сложим эти два векторных равенства:
\(\vec{PA_i} + \vec{PA_{i+1}} = (\vec{PH_i} + \vec{H_iA_i}) + (\vec{PH_i} + \vec{H_iA_{i+1}})\)
\(\vec{PA_i} + \vec{PA_{i+1}} = 2\vec{PH_i} + (\vec{H_iA_i} + \vec{H_iA_{i+1}})\)
Поскольку \(H_i\) является серединой отрезка \(A_iA_{i+1}\), векторы \(\vec{H_iA_i}\) и \(\vec{H_iA_{i+1}}\) имеют одинаковую длину, лежат на одной прямой и направлены в противоположные стороны. Следовательно, их сумма равна нулевому вектору: \(\vec{H_iA_i} + \vec{H_iA_{i+1}} = \vec{0}\).
Подставляя это в предыдущее равенство, получаем:
\(\vec{PA_i} + \vec{PA_{i+1}} = 2\vec{PH_i} + \vec{0}\)
\(\vec{PA_i} + \vec{PA_{i+1}} = 2\vec{PH_i}\)
Это соотношение справедливо для каждой боковой грани правильной шестиугольной пирамиды. Теперь просуммируем это равенство по всем шести граням (от \(i=1\) до \(i=6\)):
\(\sum_{i=1}^6 (\vec{PA_i} + \vec{PA_{i+1}}) = \sum_{i=1}^6 2\vec{PH_i}\)
Рассмотрим левую часть равенства. Сумма \(\sum_{i=1}^6 (\vec{PA_i} + \vec{PA_{i+1}})\) представляет собой сумму всех векторов боковых рёбер, где каждый вектор бокового ребра \(\vec{PA_i}\) встречается дважды: один раз в сумме для грани \(PA_{i-1}A_i\) (для \(i=1\) это грань \(PA_6A_1\)) как \(\vec{PA_i}\) и один раз в сумме для грани \(PA_iA_{i+1}\) как \(\vec{PA_i}\). Таким образом, левая часть равна удвоенной сумме всех векторов боковых рёбер:
\(\sum_{i=1}^6 (\vec{PA_i} + \vec{PA_{i+1}}) = (\vec{PA_1} + \vec{PA_2}) + (\vec{PA_2} + \vec{PA_3}) + \dots + (\vec{PA_6} +\)
\(+\vec{PA_1}) = 2\vec{PA_1} + 2\vec{PA_2} + \dots + 2\vec{PA_6} = 2\sum_{i=1}^6 \vec{PA_i}\)
Правая часть равенства равна удвоенной сумме векторов апофем:
\(\sum_{i=1}^6 2\vec{PH_i} = 2\sum_{i=1}^6 \vec{PH_i}\)
Приравнивая левую и правую части, получаем:
\(2\sum_{i=1}^6 \vec{PA_i} = 2\sum_{i=1}^6 \vec{PH_i}\)
Разделив обе части на 2, окончательно получаем:
\(\sum_{i=1}^6 \vec{PA_i} = \sum_{i=1}^6 \vec{PH_i}\)
Таким образом, сумма всех векторов с началом в точке \(P\), образованных боковыми рёбрами пирамиды, равна сумме всех векторов с началом в точке \(P\), образованных апофемами, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!