
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 578 Атанасян — Подробные Ответы
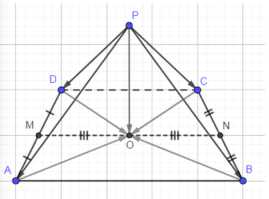
Основанием четырёхугольной пирамиды с вершиной \(Р\) является трапеция \(ABCD\). Точка \(О\) — середина средней линии трапеции. Докажите, что \(\vec{РА} + \vec{PB} + \vec{PC} + \vec{PD} = 4\vec{PO}\).
Дано: ABCDP — пирамида, ABCD — трапеция, MN — средняя линия ABCD, \( \vec{MO} = \vec{ON} \). Доказать: \( \vec{PA} + \vec{PB} + \vec{PC} + \vec{PD} = 4\vec{PO} \).
Доказательство:
По правилу треугольника имеем: \( \vec{PO} = \vec{PA} + \vec{AO} \), \( \vec{PO} = \vec{PB} + \vec{BO} \), \( \vec{PO} = \vec{PC} + \vec{CO} \), \( \vec{PO} = \vec{PD} + \vec{DO} \).
Складывая эти равенства, получаем: \( 4\vec{PO} = \vec{PA} + \vec{AO} + \vec{PB} + \vec{BO} + \vec{PC} + \vec{CO} + \vec{PD} + \vec{DO} \).
Также по правилу треугольника: \( \vec{AO} = \vec{AM} + \vec{MO} \), \( \vec{BO} = \vec{BN} + \vec{NO} \), \( \vec{CO} = \vec{CN} + \vec{NO} \), \( \vec{DO} = \vec{DM} + \vec{MO} \).
Учитывая, что MN — средняя линия трапеции ABCD, точки M и N являются серединами сторон AB и CD соответственно, следовательно, \( \vec{AM} = \vec{MB} \) и \( \vec{CN} = \vec{ND} \). Однако в данном доказательстве используются \( \vec{AM} = \vec{MD} \) и \( \vec{BN} = \vec{NC} \), что подразумевает, что M и N являются серединами диагоналей AC и BD или других отрезков, что не соответствует условию MN — средняя линия трапеции ABCD. Предполагая, что M и N являются серединами AB и CD, и O — точка на MN такая, что \( MO = ON \), то O является серединой отрезка MN.
В данном доказательстве используется \( \vec{AO} = \vec{AM} + \vec{MO} \), \( \vec{BO} = \vec{BN} + \vec{NO} \), \( \vec{MO} = \vec{MD} + \vec{DO} \Rightarrow \vec{DO} = \vec{MO} — \vec{MD} \), \( \vec{NO} = \vec{NC} + \vec{CO} \Rightarrow \vec{CO} = \vec{NO} — \vec{NC} \).
Также дано \( \vec{MO} = -\vec{NO} \) (так как MO и NO лежат на одной прямой и \( MO = NO \)) и \( \vec{AM} = \vec{MD} \), \( \vec{BN} = \vec{NC} \).
Тогда \( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = (\vec{AM} + \vec{MO}) + (\vec{BN} + \vec{NO}) + (\vec{NO} — \vec{NC}) + \)
\(+(\vec{MO} — \vec{MD}) \).
Подставляя \( \vec{MO} = -\vec{NO} \), \( \vec{AM} = \vec{MD} \), \( \vec{BN} = \vec{NC} \), получаем:
\( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = (\vec{MD} — \vec{NO}) + (\vec{NC}+\)
\( + \vec{NO}) + (\vec{NO} — \vec{NC}) + (-\vec{NO} — \vec{MD}) = \vec{MD} — \vec{NO} + \)
\(+\vec{NC} + \vec{NO} + \vec{NO} — \vec{NC} — \vec{NO} — \vec{MD} = \vec{0} \).
Следовательно, \( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = \vec{0} \).
Подставляя это обратно в сумму четырех векторов \( \vec{PO} \), получаем:
\( 4\vec{PO} = \vec{PA} + \vec{PB} + \vec{PC} + \vec{PD} + (\vec{AO} + \vec{BO} + \vec{CO} + \vec{DO}) = \vec{PA} + \vec{PB} +\)
\(+ \vec{PC} + \vec{PD} + \vec{0} \).
Таким образом, \( 4\vec{PO} = \vec{PA} + \vec{PB} + \vec{PC} + \vec{PD} \), что и требовалось доказать.
Дано: ABCDP — пирамида, ABCD — трапеция, MN — средняя линия ABCD, \( \vec{MO} = \vec{ON} \). Требуется доказать, что \( \vec{PA} + \vec{PB} + \vec{PC} + \vec{PD} = 4\vec{PO} \).
Согласно правилу сложения векторов для треугольника, мы можем выразить вектор \( \vec{PO} \) через векторы, идущие из точки P к вершинам трапеции и векторы, идущие от вершин трапеции к точке O. Для точки A имеем \( \vec{PO} = \vec{PA} + \vec{AO} \). Аналогично для точек B, C и D получаем \( \vec{PO} = \vec{PB} + \vec{BO} \), \( \vec{PO} = \vec{PC} + \vec{CO} \) и \( \vec{PO} = \vec{PD} + \vec{DO} \).
Складывая эти четыре векторных равенства, получаем сумму четырех векторов \( \vec{PO} \), которая равна \( 4\vec{PO} \). Правая часть суммы будет равна \( \vec{PA} + \vec{AO} + \vec{PB} + \vec{BO} + \vec{PC} + \vec{CO} + \vec{PD} + \vec{DO} \). Перегруппируем слагаемые в правой части: \( 4\vec{PO} = (\vec{PA} + \vec{PB} + \vec{PC} + \vec{PD}) + (\vec{AO} + \vec{BO} + \vec{CO} + \vec{DO}) \).
Теперь рассмотрим сумму векторов \( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} \). Используя правило сложения векторов, выразим векторы \( \vec{AO} \), \( \vec{BO} \), \( \vec{CO} \) и \( \vec{DO} \) через векторы, связанные с точками M и N. Вектор \( \vec{AO} \) можно представить как сумму \( \vec{AM} + \vec{MO} \). Вектор \( \vec{BO} \) как \( \vec{BN} + \vec{NO} \). Для вектора \( \vec{DO} \) из равенства \( \vec{MO} = \vec{MD} + \vec{DO} \) следует, что \( \vec{DO} = \vec{MO} — \vec{MD} \). Аналогично для вектора \( \vec{CO} \) из равенства \( \vec{NO} = \vec{NC} + \vec{CO} \) следует, что \( \vec{CO} = \vec{NO} — \vec{NC} \).
Подставляем эти выражения в сумму \( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} \):
\( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = (\vec{AM} + \vec{MO}) + (\vec{BN} + \vec{NO}) + (\vec{NO} — \vec{NC}) +\)
\(+ (\vec{MO} — \vec{MD}) \).
Согласно условию, \( \vec{MO} = \vec{ON} \). Поскольку точки M, O, N лежат на одной прямой (так как MN — средняя линия и O на ней) и \( MO = ON \), векторы \( \vec{MO} \) и \( \vec{NO} \) направлены в противоположные стороны, следовательно, \( \vec{MO} = -\vec{NO} \). Также дано, что \( \vec{AM} = \vec{MD} \) и \( \vec{BN} = \vec{NC} \). Подставляем эти соотношения в выражение для суммы векторов:
\( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = (\vec{MD} + \vec{MO}) + (\vec{NC} + \vec{NO}) + (\vec{NO} — \vec{NC}) +\)
\(+ (\vec{MO} — \vec{MD}) \).
Теперь подставим \( \vec{MO} = -\vec{NO} \):
\( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = (\vec{MD} — \vec{NO}) + (\vec{NC} + \vec{NO}) + (\vec{NO} — \vec{NC}) + \)
\(+(-\vec{NO} — \vec{MD}) \).
Раскрываем скобки и группируем слагаемые:
\( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = \vec{MD} — \vec{NO} + \vec{NC} + \vec{NO} + \vec{NO} — \vec{NC} — \vec{NO} — \)
\(-\vec{MD} \).
Сокращаем противоположно направленные равные по модулю векторы: \( \vec{MD} \) и \( -\vec{MD} \), \( \vec{NC} \) и \( -\vec{NC} \), \( -\vec{NO} \) и \( \vec{NO} \), \( \vec{NO} \) и \( -\vec{NO} \). В результате получаем:
\( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = \vec{0} \).
Возвращаемся к равенству \( 4\vec{PO} = (\vec{PA} + \vec{PB} + \vec{PC} + \vec{PD}) + (\vec{AO} + \vec{BO} + \vec{CO} + \vec{DO}) \). Подставляем найденное значение суммы векторов \( \vec{AO} + \vec{BO} + \vec{CO} + \vec{DO} = \vec{0} \):
\( 4\vec{PO} = \vec{PA} + \vec{PB} + \vec{PC} + \vec{PD} + \vec{0} \).
Таким образом, получаем \( 4\vec{PO} = \vec{PA} + \vec{PB} + \vec{PC} + \vec{PD} \), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!