Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 576 Атанасян — Подробные Ответы
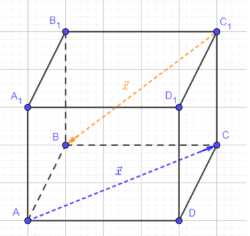
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Укажите вектор \(\vec{x}\), начало и конец которого являются вершинами параллелепипеда, такой, что: а) \(\vec{DC} + \vec{D_1A_1} + \vec{CD_1} + \vec{x} + \vec{A_1C_1} = \vec{DB}\); б) \(\vec{DА} + \vec{x} + \vec{D_1B} + \vec{AD_1} + \vec{BА} = \vec{DС}\).
а) \(\vec{DC} + \vec{D_1A_1} + \vec{CD_1} + \vec{x} + \vec{A_1C_1} = \vec{DB}\). Группируем векторы: \((\vec{DC} + \vec{CD_1} + \vec{D_1A_1} + \vec{A_1C_1}) + \vec{x} = \vec{DB}\). Используя свойства параллелепипеда \(\vec{D_1A_1} = \vec{DA}\) и \(\vec{A_1C_1} = \vec{AC}\), а также правило сложения векторов, получаем \(\vec{DC} + \vec{CD_1} = \vec{DD_1}\) и \(\vec{D_1A_1} + \vec{A_1C_1} = \vec{D_1C_1}\). Тогда \((\vec{DC} + \vec{CD_1} + \vec{D_1A_1} + \vec{A_1C_1}) = \vec{DD_1} + \vec{D_1C_1} = \vec{DC_1}\). Уравнение принимает вид \(\vec{DC_1} + \vec{x} = \vec{DB}\). Отсюда \(\vec{x} = \vec{DB} — \vec{DC_1}\). Вектор разности \(\vec{DB} — \vec{DC_1}\) равен вектору \(\vec{C_1B}\). Таким образом, \(\vec{x} = \vec{C_1B}\).
б) \(\vec{DА} + \vec{x} + \vec{D_1B} + \vec{AD_1} + \vec{BА} = \vec{DС}\). Группируем векторы: \((\vec{DA} + \vec{AD_1} + \vec{D_1B} + \vec{BA}) + \vec{x} = \vec{DC}\). Используя правило сложения векторов: \(\vec{DA} + \vec{AD_1} = \vec{DD_1}\), \(\vec{DD_1} + \vec{D_1B} = \vec{DB}\), \(\vec{DB} + \vec{BA} = \vec{DA}\). Таким образом, \((\vec{DA} + \vec{AD_1} + \vec{D_1B} + \vec{BA}) = \vec{DA}\). Уравнение принимает вид \(\vec{DA} + \vec{x} = \vec{DC}\). Отсюда \(\vec{x} = \vec{DC} — \vec{DA}\). Вектор разности \(\vec{DC} — \vec{DA}\) равен вектору \(\vec{AC}\). Таким образом, \(\vec{x} = \vec{AC}\).
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Требуется найти вектор \(\vec{x}\), который соединяет две вершины параллелепипеда, исходя из двух данных векторных уравнений.
а) Первое уравнение: \(\vec{DC} + \vec{D_1A_1} + \vec{CD_1} + \vec{x} + \vec{A_1C_1} = \vec{DB}\).
Для начала сгруппируем известные векторы в левой части уравнения: \((\vec{DC} + \vec{D_1A_1} + \vec{CD_1} + \vec{A_1C_1}) + \vec{x} = \vec{DB}\).
В параллелепипеде противоположные грани параллельны и равны, а соответствующие ребра параллельны и равны по длине. Также векторы, направленные вдоль параллельных и равных отрезков в одном направлении, равны.
Рассмотрим сумму векторов в скобках. Переставим слагаемые для удобства, используя коммутативность сложения векторов: \((\vec{DC} + \vec{CD_1}) + (\vec{D_1A_1} + \vec{A_1C_1}) + \vec{x} = \vec{DB}\).
Применяем правило треугольника или многоугольника для сложения векторов: \(\vec{DC} + \vec{CD_1}\) представляет собой вектор, идущий из точки \(D\) в точку \(C_1\), то есть \(\vec{DD_1}\).
Аналогично, \(\vec{D_1A_1} + \vec{A_1C_1}\) представляет собой вектор, идущий из точки \(D_1\) в точку \(C_1\), то есть \(\vec{D_1C_1}\).
Тогда сумма в скобках становится: \(\vec{DD_1} + \vec{D_1C_1}\). Снова применяя правило треугольника, эта сумма равна вектору, идущему из точки \(D\) в точку \(C_1\), то есть \(\vec{DC_1}\).
Таким образом, исходное уравнение упрощается до вида: \(\vec{DC_1} + \vec{x} = \vec{DB}\).
Чтобы найти вектор \(\vec{x}\), выразим его из этого уравнения: \(\vec{x} = \vec{DB} — \vec{DC_1}\).
По правилу вычитания векторов, разность \(\vec{DB} — \vec{DC_1}\) равна вектору, идущему из конца вычитаемого вектора (\(C_1\)) к концу уменьшаемого вектора (\(B\)). Следовательно, \(\vec{x} = \vec{C_1B}\).
б) Второе уравнение: \(\vec{DА} + \vec{x} + \vec{D_1B} + \vec{AD_1} + \vec{BА} = \vec{DС}\).
Сгруппируем известные векторы: \((\vec{DА} + \vec{D_1B} + \vec{AD_1} + \vec{BА}) + \vec{x} = \vec{DС}\).
Переставим слагаемые в скобках для удобства сложения по правилу многоугольника: \((\vec{DА} + \vec{AD_1} + \vec{D_1B} + \vec{BА}) + \vec{x} = \vec{DС}\).
Складываем векторы последовательно:
\(\vec{DА} + \vec{AD_1}\) дает вектор \(\vec{DD_1}\) (из \(D\) в \(D_1\)).
\(\vec{DD_1} + \vec{D_1B}\) дает вектор \(\vec{DB}\) (из \(D\) в \(B\)).
\(\vec{DB} + \vec{BA}\) дает вектор \(\vec{DA}\) (из \(D\) в \(A\)).
Таким образом, сумма всех векторов в скобках равна \(\vec{DA}\).
Уравнение принимает вид: \(\vec{DA} + \vec{x} = \vec{DC}\).
Выражаем вектор \(\vec{x}\): \(\vec{x} = \vec{DC} — \vec{DA}\).
По правилу вычитания векторов, разность \(\vec{DC} — \vec{DA}\) равна вектору, идущему из конца вычитаемого вектора (\(A\)) к концу уменьшаемого вектора (\(C\)). Следовательно, \(\vec{x} = \vec{AC}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.