
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 575 Атанасян — Подробные Ответы
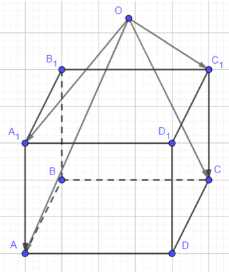
Дан параллелепипед \(ABCDA_1B_1C_1D_1\). Докажите, что \(\vec{ОА} + \vec{ОС_1} = \vec{ОС} + \vec{ОА_1}\), где \(О\) — произвольная точка пространства.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед; \(О\) — произвольная точка. Доказать: \(\vec{ОА} + \vec{ОС_1} = \vec{ОС} + \vec{ОА_1}\). Доказательство: \(\vec{ОА} = \vec{ОА_1} + \vec{А_1А}\), отсюда \(\vec{А_1А} = \vec{ОА} — \vec{ОА_1}\); \(\vec{ОС} = \vec{ОС_1} + \vec{С_1С}\), отсюда \(\vec{С_1С} = \vec{ОС} — \vec{ОС_1}\); \(\vec{А_1А} = \vec{С_1С}\) (так как \(\vec{А_1А} \parallel \vec{С_1С}\) и \(А_1А = С_1С\)); Таким образом: \(\vec{ОА} — \vec{ОА_1} = \vec{ОС} — \vec{ОС_1} \Rightarrow \vec{ОА} + \vec{ОС_1} = \vec{ОС} + \vec{ОА_1}\), что и требовалось доказать.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед; \(О\) — произвольная точка пространства. Требуется доказать, что \(\vec{ОА} + \vec{ОС_1} = \vec{ОС} + \vec{ОА_1}\).
Первый шаг доказательства состоит в выражении вектора \(\vec{ОА}\) через сумму векторов, исходящих из точки \(О\). Используя правило сложения векторов, можно записать \(\vec{ОА} = \vec{ОА_1} + \vec{А_1А}\). Из этого векторного равенства можно выразить вектор \(\vec{А_1А}\) как разность векторов \(\vec{ОА}\) и \(\vec{ОА_1}\), то есть \(\vec{А_1А} = \vec{ОА} — \vec{ОА_1}\).
Второй шаг аналогичен первому, но применяется к вектору \(\vec{ОС}\). Вектор \(\vec{ОС}\) может быть представлен как сумма векторов \(\vec{ОС_1}\) и \(\vec{С_1С}\): \(\vec{ОС} = \vec{ОС_1} + \vec{С_1С}\). Выражая из этого равенства вектор \(\vec{С_1С}\), получаем \(\vec{С_1С} = \vec{ОС} — \vec{ОС_1}\).
Третий шаг основан на свойствах параллелепипеда. В параллелепипеде противоположные ребра параллельны и равны по длине. Векторы, соответствующие этим ребрам, равны. В данном случае, ребро \(А_1А\) параллельно и равно ребру \(С_1С\). Следовательно, векторы \(\vec{А_1А}\) и \(\vec{С_1С}\) равны: \(\vec{А_1А} = \vec{С_1С}\). Это равенство векторов следует из того, что отрезки \(А_1А\) и \(С_1С\) параллельны (\(А_1А \parallel С_1С\)) и имеют одинаковую длину (\(А_1А = С_1С\)).
Четвертый шаг объединяет результаты предыдущих шагов. Поскольку \(\vec{А_1А} = \vec{С_1С}\), мы можем приравнять выражения для этих векторов, полученные на первом и втором шагах: \(\vec{ОА} — \vec{ОА_1} = \vec{ОС} — \vec{ОС_1}\). Перенося векторы с индексом «1» в правую часть уравнения, а векторы без индекса «1» в левую часть, получаем \(\vec{ОА} + \vec{ОС_1} = \vec{ОС} + \vec{ОА_1}\). Это именно то равенство, которое требовалось доказать. Таким образом, доказательство завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!