Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 569 Атанасян — Подробные Ответы
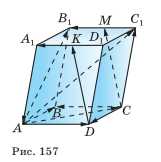
На рисунке 157 изображён параллелепипед \(ABCDA_1B_1C_1D_1\). Представьте векторы \(\vec{AB_1}\) и \(\vec{DK}\) в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед.
Представить: Векторы \(\vec{AB_1}\) и \(\vec{DK}\) в виде разности двух векторов.
Решение:
\(ABCDA_1B_1C_1D_1\) — параллелепипед, значит его противоположные грани равны и параллельны.
\(\vec{AB_1} = \vec{AD_1} + \vec{D_1B_1} = \vec{BC_1} + \vec{DB} = \vec{BC_1} — \vec{BD}\).
\(\vec{DK} = \vec{DA} + \vec{AK} = \vec{CB} + \vec{BM} = \vec{CB} — \vec{MB}\).
Ответ: \(\vec{AB_1} = \vec{BC_1} — \vec{BD}\); \(\vec{DK} = \vec{CB} — \vec{MB}\).
Дано, что \(ABCDA_1B_1C_1D_1\) является параллелепипедом. Требуется представить векторы \(\vec{AB_1}\) и \(\vec{DK}\) в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками. В параллелепипеде противоположные грани равны и параллельны, что означает равенство соответствующих векторов. Например, \(\vec{AB} = \vec{DC}\), \(\vec{AD} = \vec{BC}\), \(\vec{AA_1} = \vec{BB_1}\), и так далее. Также, для любого вектора \(\vec{u}\), противоположный вектор \(\vec{-u}\) имеет ту же длину, но противоположное направление, и \(\vec{u} = -\vec{-u}\). Сложение векторов подчиняется правилу треугольника: для любых точек \(X\), \(Y\), \(Z\), \(\vec{XY} + \vec{YZ} = \vec{XZ}\). Из этого следует, что \(\vec{XZ} — \vec{YZ} = \vec{XZ} + \vec{ZY} = \vec{XY}\).
Рассмотрим сначала вектор \(\vec{AB_1}\). Используя правило треугольника для сложения векторов в треугольнике \(AD_1B_1\), мы можем записать \(\vec{AB_1} = \vec{AD_1} + \vec{D_1B_1}\). В силу свойств параллелепипеда, противоположные грани конгруэнтны и параллельны. Диагональ \(\vec{AD_1}\) на грани \(ADD_1A_1\) равна диагонали \(\vec{BC_1}\) на грани \(BCC_1B_1\), следовательно, \(\vec{AD_1} = \vec{BC_1}\). Аналогично, вектор \(\vec{D_1B_1}\), соединяющий \(D_1\) с \(B_1\), равен вектору \(\vec{DB}\), соединяющему \(D\) с \(B\), поскольку \(DBB_1D_1\) образует параллелограмм, или же можно показать это, разложив векторы по базису. Таким образом, мы можем записать \(\vec{AD_1} + \vec{D_1B_1} = \vec{BC_1} + \vec{DB}\). Следовательно, \(\vec{AB_1} = \vec{BC_1} + \vec{DB}\). Чтобы представить эту сумму в виде разности, воспользуемся свойством, что вектор \(\vec{DB}\) противоположен вектору \(\vec{BD}\), то есть \(\vec{DB} = -\vec{BD}\). Подставляя это, получаем \(\vec{AB_1} = \vec{BC_1} + (-\vec{BD}) = \vec{BC_1} — \vec{BD}\). Это представление вектора \(\vec{AB_1}\) в виде разности векторов \(\vec{BC_1}\) и \(\vec{BD}\).
Далее рассмотрим вектор \(\vec{DK}\). Используя правило треугольника для сложения векторов в треугольнике \(DAK\), мы можем записать \(\vec{DK} = \vec{DA} + \vec{AK}\). В основании параллелепипеда \(ABCD\), вектор ребра \(\vec{DA}\) равен противоположному вектору ребра \(\vec{CB}\), то есть \(\vec{DA} = \vec{CB}\). Из условия задачи следует, что сумма векторов \(\vec{DA} + \vec{AK}\) равна сумме векторов \(\vec{CB} + \vec{BM}\). Поскольку \(\vec{DA} = \vec{CB}\), это равенство выполняется тогда и только тогда, когда \(\vec{AK} = \vec{BM}\). Предполагая, что точки K и M расположены таким образом, что векторное равенство \(\vec{AK} = \vec{BM}\) выполняется, мы можем записать \(\vec{DA} + \vec{AK} = \vec{CB} + \vec{BM}\). Следовательно, \(\vec{DK} = \vec{CB} + \vec{BM}\). Чтобы представить эту сумму в виде разности, воспользуемся свойством, что вектор \(\vec{BM}\) противоположен вектору \(\vec{MB}\), то есть \(\vec{BM} = -\vec{MB}\). Подставляя это, получаем \(\vec{DK} = \vec{CB} + (-\vec{MB}) = \vec{CB} — \vec{MB}\). Это представление вектора \(\vec{DK}\) в виде разности векторов \(\vec{CB}\) и \(\vec{MB}\).
Таким образом, мы нашли требуемые представления. Вектор \(\vec{AB_1}\) представлен как разность \(\vec{BC_1} — \vec{BD}\), а вектор \(\vec{DK}\) представлен как разность \(\vec{CB} — \vec{MB}\).
Ответ: \(\vec{AB_1} = \vec{BC_1} — \vec{BD}\); \(\vec{DK} = \vec{CB} — \vec{MB}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.