
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 567 Атанасян — Подробные Ответы
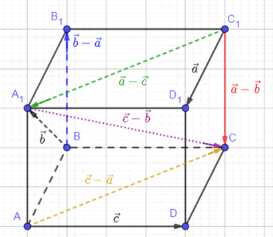
Нарисуйте параллелепипед \(ABCDA_1B_1C_1D_1\) и обозначьте векторы \(\vec{C_1D_1}\), \(\vec{BA_1}\), \(\vec{AD}\) соответственно через \(\vec{a}\), \(\vec{b}\), \(\vec{c}\). Изобразите на рисунке векторы: а) \(\vec{a} — \vec{b}\); б) \(\vec{a} — \vec{c}\); в) \(\vec{b} — \vec{a}\); г) \(\vec{c} — \vec{b}\); д) \(\vec{c} — \vec{a}\).
а) так как \(\vec{BA_1} = \vec{b}\), то \(\vec{A_1B} = -\vec{b}\); тогда \(\vec{a} — \vec{b} = \vec{C_1D_1} + \vec{A_1B} = \vec{C_1D_1} + \vec{D_1C} = \vec{C_1C}\)
б) так как \(\vec{AD} = \vec{c}\), то \(\vec{DA} = -\vec{c}\); тогда \(\vec{a} — \vec{c} = \vec{C_1D_1} + \vec{DA} = \vec{C_1D_1} + \vec{D_1A_1} = \vec{C_1A_1}\)
в) так как \(\vec{C_1D_1} = \vec{a}\), то \(\vec{D_1C_1} = -\vec{a}\); тогда \(\vec{b} — \vec{a} = \vec{BA_1} + \vec{D_1C_1} = \vec{BA_1} + \vec{A_1B_1} = \vec{BB_1}\)
г) так как \(\vec{BA_1} = \vec{b}\), то \(\vec{A_1B} = -\vec{b}\); тогда \(\vec{c} — \vec{b} = \vec{AD} + \vec{A_1B} = \vec{A_1D_1} + \vec{A_1B} = \vec{A_1C}\) (по правилу параллелограмма)
д) так как \(\vec{C_1D_1} = \vec{a}\), то \(\vec{D_1C_1} = -\vec{a}\); тогда \(\vec{c} — \vec{a} = \vec{AD} + \vec{D_1C_1} = \vec{AD} + \vec{DC} = \vec{AC}\)
C_1}\). I will mention that \(\vec{A_1C}\) is the diagonal of the face \(A_1Для решения данной задачи, используем свойства векторов в параллелепипеде и правила сложения и вычитания векторов. В параллелепипеде противоположные ребра параллельны и равны по длине, что означает равенство соответствующих векторов. Также будем использовать правило треугольника и правило параллелограмма для сложения векторов.
а) Найдем вектор \(\vec{a} — \vec{b}\).
Нам даны векторы \(\vec{a} = \vec{C_1D_1}\) и \(\vec{b} = \vec{BA_1}\).
Вычитание вектора можно заменить сложением с противоположным вектором: \(\vec{a} — \vec{b} = \vec{a} + (-\vec{b})\).
Вектор \(-\vec{b}\) является вектором, противоположным вектору \(\vec{BA_1}\), то есть \(\vec{A_1B}\).
Таким образом, нам необходимо найти сумму векторов \(\vec{C_1D_1} + \vec{A_1B}\).
В параллелепипеде ребро \(A_1B\) параллельно и равно ребру \(D_1C\),
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!